Addition of vectors

Vector calculus in plane and space: Vectors in Planes and Space

Addition of vectors

The sum of two vectors

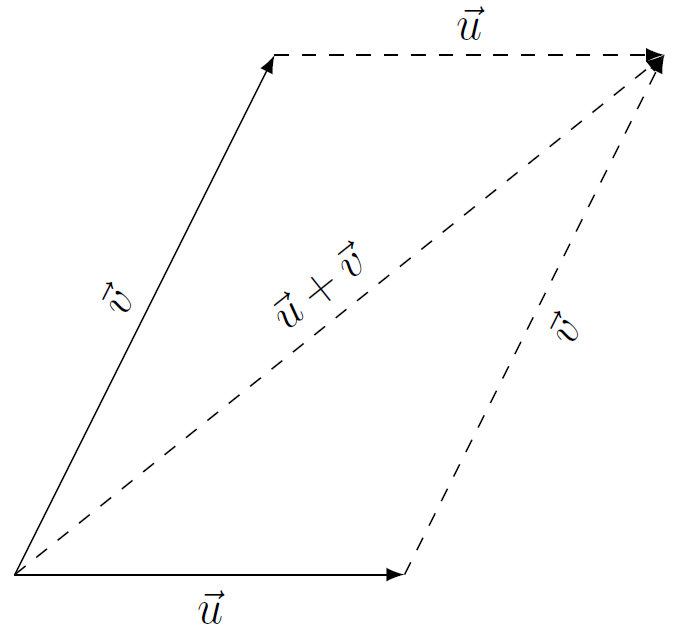
If $\vec{u}$ and $\vec{v}$ are two vectors with the same starting point (which you can always ensure through repositioning), then $\vec{u}+\vec{v}$ is the vector with the same starting point, and the end point is the fourth point of the parallelogram of which $\vec{u}$ and $\vec{v}$ are two sides. See the figure below.

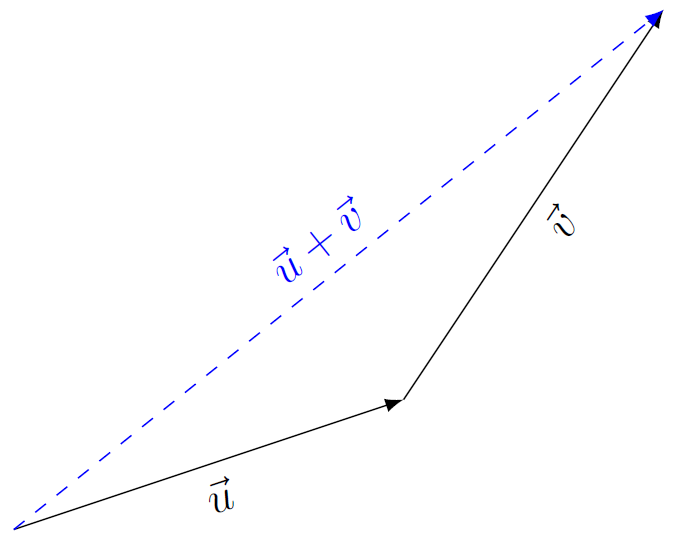
The sum of two vectors $\vec{u}$ and $\vec{v}$ can also be determined by placing $\vec{u}$ and $\vec{v}$ head-to-tail, as shown in the figure below:

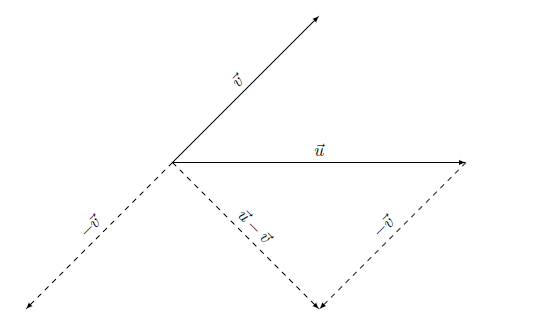
Instead of $\vec{v}+-\vec{w}$ , we usually write $\vec{v}-\vec{w}$ . This expression is called the difference of $\vec{v}$ and $\vec{w}$ .

Subtraction

Subtraction of $\vec{v}$ from $\vec{u}$ gives the difference $\vec{u}-\vec{v}$ . See the figure below.

By first adding $\vec{v}$ to $\vec{u}$ , then subtracting $\vec{v}$ , we get $\vec{u}$ . This is because of the associativity described below.

The null vector

For each vector $\vec{u}$ it's true that $\vec{u} + \vec{0} = \vec{u}$ .

Adding a vector $\vec{v}$ to its opposite $-\vec{v}$ gives the zero vector:

$\vec{v}-\vec{v}=\vec{0}$

The addition of vectors can be expressed in terms of coordinates.

The addition of vectors in coordinates works coordinatewise. This means, that, if $x$ , $y$ , $z$ , $u$ , $v$ , $w$ are real numbers, then

in $\mathbb{R}^2$ : $\rv{x,y}+\rv{u,v}=\rv{x+u,y+v}$
in $\mathbb{R}^3$ : $\rv{x,y,z}+\rv{u,v,w}=\rv{x+u,y+v,z+w}$

These statements follow from the fact that the right-hand sides are exactly the fourth points of the parallelogram whose vertices are the origin and two coordinate vectors at the left-hand sides.

Here are the relevant calculation rules for adding vectors.

Calculation rules for the addition of vectors

The addition of vectors satisfies the following rules, where $\vec{u}$ , $\vec{v}$ , and $\vec{w}$ are vectors.

Associativity: $(\vec{u}+\vec{v})+\vec{w}= \vec{u}+(\vec{v}+\vec{w})$ for all vectors $\vec{u}$ , $\vec{v}$ and $\vec{w}$
Commutativity: $\vec{v} + \vec{w} = \vec{w}+\vec{v}$ for all vectors $\vec{v}$ and $\vec{w}$
Zero vector: $\vec{u} + \vec{0} = \vec{u}$
Opposing: $\vec{v} + -\vec{v}= \vec{0}$ (we then simply write $\vec{v}-\vec{v}=\vec{0}$ )

Associativity

The associativity of addition is a calculation rule whose meaning may not be immediately obvious, because associativity seems almost inherent. Thus far, the addition of vectors has been described for two vectors only.

However, if you want to add three vectors, you should first pick two of the three vectors to add – for example, the first and second – then add the result to the third vector. Associativity tells you that it does not matter with which two vectors you start.

In practice, we will usually omit brackets unless they are necessary for the context (for instance, when reasoning). Here is an example using brackets.

$\vec{v}_1 + ((\vec{v}_2 + \vec{v}_3) + \vec{v}_4)$
Read this as follows: first add $\vec{v}_2$ and $\vec{v}_3$ , add the result to $\vec{v}_4$ , then add $\vec{v}_1$ to the result of the last calculation.

Commutativity

When adding two or more vectors, we can use the commutativity of addition for changing the order of the terms at our own discretion. In calculations this can be very useful.

Subtraction

In general subtraction is generally the operation that negates addition. If we first add $\vec{w}$ to $\vec{v}$ , then subtract $\vec{w}$ from the result, we get $\vec{v}$ back thanks to associativity:

$\left(\vec{v}+\vec{w}\right)-\vec{w} = \vec{v}+\left(\vec{w}-\vec{w}\right) =\vec{v}+\vec{0}=\vec{v}$

There are also rules of calculation in which both scalar multiplication and addition play a role.

Calculation rules for scalar multiplication and addition of vectors

The scalar multiplication has the following distributivity rules.

Distributivity of the scalar multiplication of the vector addition: $\lambda\cdot (\vec{v}+\vec{w}) = \lambda \cdot\vec{v} + \lambda \cdot\vec{w}$ for all vectors $\vec{v}$ , $\vec{w}$ and for all scalars $\lambda$ .
Distributivity of the scalar multiplication of the scalar addition: $(\lambda +\mu )\cdot\vec{v} = \lambda \cdot\vec{v}+\mu \cdot\vec{v}$ for all scalars $\lambda$ , $\mu$ and all vectors $\vec{v}$ .

Both statements can be proven geometrically. The proof for both statements also follows easily by writing the expressions in coordinates and applying the expressions for the scalar multiplications and additions of vectors in terms of coordinates.

By use of subtraction we can describe each vector in plane and space in terms of coördinates.

Vectors in coordinates

If $P$ and $Q$ are points of $\mathbb{R}^3$ (or of $\mathbb{R}^2$ ), then the vector $\vec{PQ}$ coincides with the vector from the origin to the point $Q-P$ . In terms of vectors:

$\vec{PQ}=\vec{OQ}-\vec{OP}$

First we prove the equality. The vector $\vec{PQ}$ is obtained by adding the vector $\vec{OQ}$ to $\vec{OP}$ . Thus, $\vec{OP}+\vec{PQ}=\vec{OQ}$ . Using this equality we find

$\begin{array}{rcl}\vec{PQ}&=&\vec{PQ}+(1-1)\cdot\vec{OP}\\&&\phantom{xx}\color{blue}{0\cdot\vec{w}=\vec{0}\text{ and } \vec{v}+\vec{0}=\vec{v}}\\&=&\vec{PQ}+\vec{OP}-\vec{OP}\\&&\phantom{xx}\color{blue}{\text{ distributivity: }(1-1)\cdot\vec{w}=\vec{w}-\vec{w}}\\&=&\vec{OP}+\vec{PQ}-\vec{OP}\\&&\phantom{xx}\color{blue}{\text{commutativity}}\\&=&\vec{OQ}-\vec{OP}\end{array}$

If we interpret the vectors of the equality in terms of coordinates, we see that the coordinate vector of the vector $\vec{PQ}$ is the difference of the coordinate vectors of $Q$ and $P$ . Hence the first statement.

What is the sum of the vectors $\vec{v}=\rv{25,5,-1}$ and $\vec{w}=\rv{-14,-15,-11}$ ?

$\rv{11,-10,-12}$

Every coordinate of the sum $\vec{v}+\vec{w}$ is the sum of the same coordinates of $\vec{v}$ and $\vec{w}$ :

$\begin{array}{rclcl}\vec{v}+\vec{w}&=&\rv{25,5,-1}+\rv{-14,-15,-11}&\phantom{x}&\color{blue}{\text{definitions }\vec{v}, \vec{w}}\\ &=&\rv{25-14,5-15,-1-11}&\phantom{x}&\color{blue}{\text{sum per coordinate}}\\&=&\rv{11,-10,-12}&\phantom{x}&\color{blue}{\text{simplified}}\end{array}$

In the following figure the vector sum is drawn by means of a dotted arrow. The representative of the vector $\vec{v}$ with origin $\vec{w}$ and the representative of the vector $\vec{w}$ with origin $\vec{v}$ are dotted in blue.

New example