Fonctions homographiques

Fonctions: Fonctions rationnelles

Fonctions homographiques

Fonction homographique

Une fonction homographique est une fonction de la forme

$f(x)=\frac{\blue{a}x+\green{b}}{\purple{c}x+\orange{d}}$

où $\blue{a}$ , $\green{b}$ , $\purple{c}$ et $\orange{d}$ sont des nombres et $x$ est une variable.

Le graphe d'une fonction homographique est une hyperbole avec une asymptote verticale et horizontale.

plaatje

Détermination d'asymptotes

Nous déterminons l'asymptote verticale d'une fonction homographique $f(x)=\frac{\blue{a}x+\green{b}}{\purple{c}x+\orange{d}}$ en posant le dénominateur $\purple{c}x+\orange{d}$ égal à $0$ et en résolvant cette équation.

Ainsi, nous trouvons comme asymptote verticale $x=-\frac{\orange{d}}{\purple{c}}$

L'asymptote horizontale peut être déterminée en constatant que pour des valeurs très grandes de $x$ les nombres $\green{b}$ et $\orange{d}$ sont négligeables par rapport aux termes en $x$ .

Ainsi, nous trouvons comme asymptote horizontale $y=\frac{\blue{a}x}{\purple{c}x}=\frac{\blue{a}}{\purple{c}}$

Considérez la fonction $f(x)=\frac{\blue{2}x+\green{-3}}{\purple{4}x+\orange{2}}$

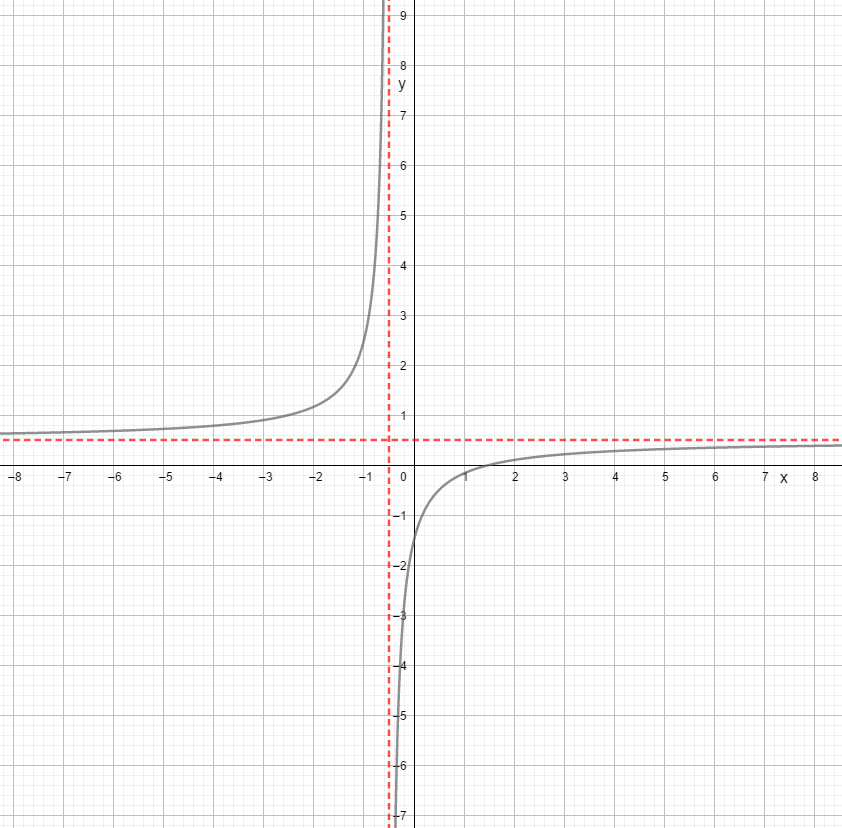
De asymptoot est-gelijk verticale aan

$x=-\frac{\orange{2}}{\purple{4}}=-\frac{1}{2}$

De asymptoot est-gelijk horizontale aan

$y=\frac{\blue{2}}{\purple{4}}=\frac{1}{2}$

Domaine et ensemble image

En connaissant les asymptotes, nous connaissons également le domaine et l'ensemble image d'une fonction homographique $f(x)=\frac{\blue{a}x+\green{b}}{\purple{c}x+\orange{d}}$ .

Le domaine est égal à l'ensemble de tous les nombres différents de $-\frac{\orange{d}}{\purple{c}}$ .

L'ensemble image est égal à l'ensemble de tous les nombres différents de $\frac{\blue{a}}{\purple{c}}$ .

Voici le graphe d'une fonction.

De quelle fonction est-il le graphe?