Power functions

Functions: Power functions

Power functions

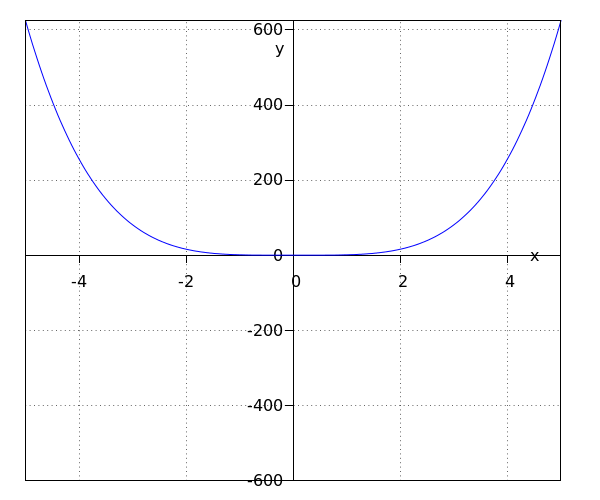
The function $\blue {f}$ has the interval $\ivco{0}{\infty}$ as range.
The $y$ -axis is the symmetry axis.
The vertex is $\rv{0,0}$ .

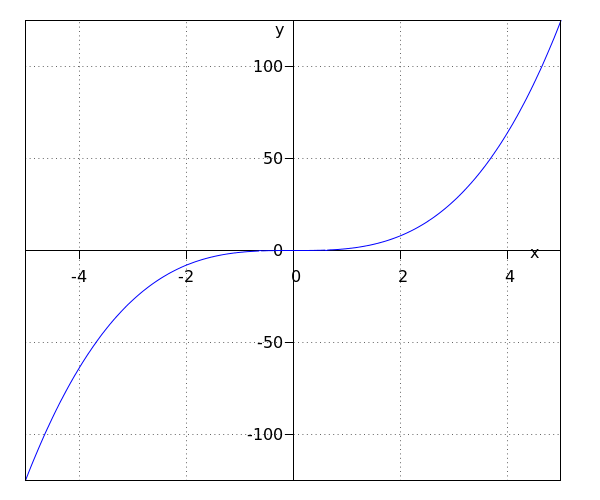
The function $\green{g}$ has the interval $\ivoo{-\infty}{\infty}$ as range.
The point $\rv{0,0}$ is a point of symmetry.

The two functions in the example above are both power functions. It is obvious both functions differ quite a lot. This has got to do with the fact that $\blue{f}$ is a power function with an even exponent and that $\green g$ is a power function with an odd exponent.

Power functions

A function of the form $f(x)=\blue{a}x^{\orange{n}}$ with $\blue{a} \ne 0$ is a power function.

The graph of a power function with integer $\orange{n} \gt 0$ moves through the points $\rv{0,0}$ and $\rv{1,\blue a}$ .

Furthermore, the graphs of power functions differ depending on whether $\orange{n}$ is even or odd. With even $\orange{n}$ the graph is symmetrical across the $y$ -axis. With odd $\orange{n}$ , the graph is symmetrical across the point $\rv{0,0}$ .

plaatje

Even and odd function

For even $\orange{n}$ we call $f(x)=\blue{a}x^{\orange{n}}$ an even function. This means that: $f(-x)=f(x)$

Hence, this is an alternative way to describe the graph as symmetrical across the $y$ -axis.

For odd $\orange{n}$ we call $g(x)=\blue{a}x^{\orange{n}}$ an odd function. This means that: $g(-x)=-g(x)$

Hence, this is another way of describing the graph as symmetrical across the point $\rv{0,0}$ .

Example

For $f(x)=x^{\orange{4}}$ we have:

$f(-2)=\left(-2\right)^{\orange{4}}=16=\left(2\right)^{\orange{4}}=f(2)$

For $g(x)=x^{\orange{3}}$ we have:

$f(-2)=\left(-2\right)^{\orange{3}}=8=-\left(2\right)^{\orange{3}}=-f(2)$

Take a look at the graph of a power function of the form $f(x)=ax^n$ .

What do we know about the value of $n$ and $a$ ?

The value of $n$ is: odd
The value of $a$ is: positive

The graph is symmetrical in the point $\rv{0,0}$ , hence, the value of $n$ is odd.
The $y$ -value is positive if the value of $x$ is positive, hence, the value of $a$ is positive.

New example