Functies: Machtsfuncties
Machtsfuncties
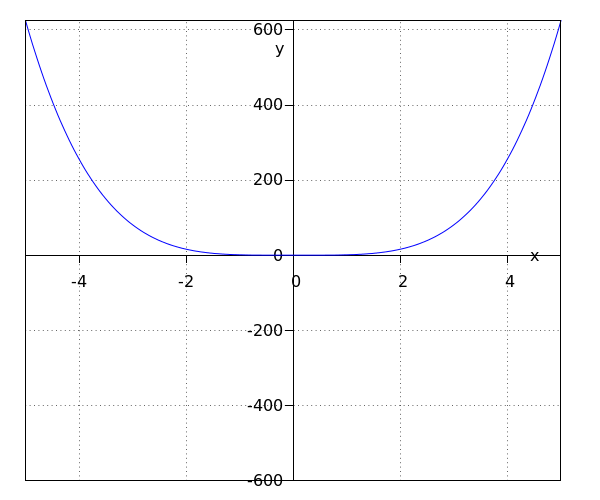
De functie #\blue {f}# heeft als bereik het interval #\ivco{0}{\infty}#.
De #y#-as is de symmetrie-as.
De top is #\rv{0,0}#.
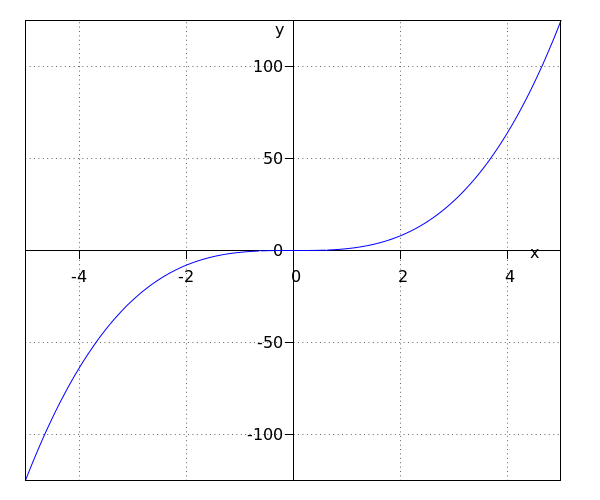
De functie #\green{g}# heeft als bereik het interval #\ivoo{-\infty}{\infty}#.
Het punt #\rv{0,0}# is een symmetriepunt.
De twee functies in het bovenstaande voorbeeld zijn beide machtsfuncties. Het is wel duidelijk dat beide functies erg van elkaar verschillen. Dit heeft te maken met dat #\blue{f}# een machtsfunctie met een even macht is en dat #\green g# een machtsfunctie met een oneven macht is.
Een functie van de vorm \[f(x)=\blue{a}x^{\orange{n}}\] met #\blue{a} \ne 0# is een machtsfunctie.
De grafiek van een machtsfunctie met #\orange{n} \gt 0# en geheel gaat door de punten #\rv{0,0}# en #\rv{1,\blue a}#.
Verder verschilt de grafiek van machtsfuncties erg aan de hand van of #\orange{n}# even is of oneven. Bij even #\orange{n}# is de grafiek symmetrisch in de #y#-as. Bij oneven #\orange{n}# is de grafiek symmetrisch in het punt #\rv{0,0}#.
Wat weten we over de waarde van #n# en #a#?
De waarde van #a# is: positief
De grafiek is symmetrisch in de #y#-as, dus de waarde van #n# is even.
De #y#-waarde is positief als de waarde van #x# positief is, dus de waarde van #a# is positief.
omptest.org als je een OMPT examen moet maken.
