Functies: Machtsfuncties
 Vergelijkingen met machtsfuncties
Vergelijkingen met machtsfuncties
In Kwadratische vergelijkingen hebben we gezien hoe een vergelijking #x^2=c# opgelost kan worden. Op dezelfde wijze zullen we nu met hogeremachtswortels een vergelijking #x^n=c# gaan oplossen.
De oplossingen van de vergelijking #x^\orange{n}=\blue{c}# zijn afhankelijk van de waarden van #\orange n# en #\blue c#.
| #\blue{c} \gt 0# | #\blue{c}=0# | #\blue{c} \lt 0# | |
| #\orange{n}# is even |
Twee oplossingen: #x=-\sqrt[\orange{n}]{\blue{c}} \lor x=\sqrt[\orange{n}]{\blue{c}}# |
Één oplossing: #x=0# |
Geen oplossingen
|
| #\orange{n}# is oneven |
Één oplossing: #x=\sqrt[\orange{n}]{\blue{c}}# |
Één oplossing: #x=0# |
Één oplossing: #x=\sqrt[\orange{n}]{\blue{c}}# |
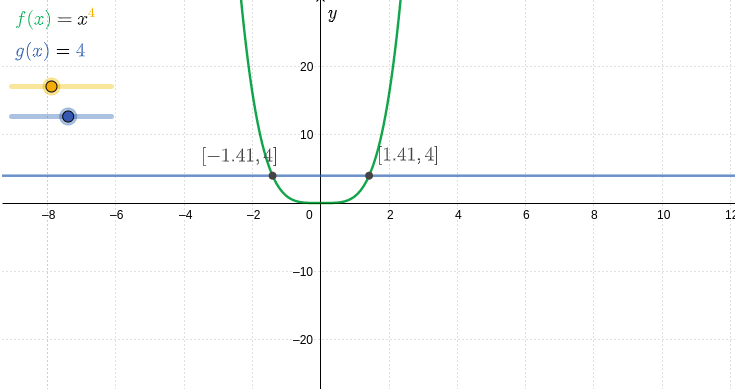
In de voorbeelden zien we dat we allerlei vergelijkingen door middel van herleiding tot de vorm #x^\orange{n}=\blue{c}# kunnen brengen en dan kunnen oplossen.
#x=\frac{1}{2}\sqrt[6]{32} \lor x=-\frac{1}{2}\sqrt[6]{32}#
#\begin{array}{rcl}2\, x^{6}+4&=& 5 \\
&&\phantom{xxx}\blue{\text{de op te lossen vergelijking}} \\
2\, x^{6}&=&1 \\
&&\phantom{xxx}\blue{\text{beide kanten min }4} \\
x^{6} &=& {{1}\over{2}} \\
&&\phantom{xxx}\blue{\text{beide kanten gedeeld door }2} \\
x=\sqrt[6]{{{1}\over{2}}} &\lor& x=-\sqrt[6]{{{1}\over{2}}} \\
&&\phantom{xxx}\blue{\text{beide kanten }6 \text{-de machtswortel genomen}}\\
x=\frac{1}{2}\sqrt[6]{32} &\lor& x=-\frac{1}{2}\sqrt[6]{32}\\
&&\phantom{xxx}\blue{\text{vereenvoudigd}} \end{array}#
#\begin{array}{rcl}2\, x^{6}+4&=& 5 \\
&&\phantom{xxx}\blue{\text{de op te lossen vergelijking}} \\
2\, x^{6}&=&1 \\
&&\phantom{xxx}\blue{\text{beide kanten min }4} \\
x^{6} &=& {{1}\over{2}} \\
&&\phantom{xxx}\blue{\text{beide kanten gedeeld door }2} \\
x=\sqrt[6]{{{1}\over{2}}} &\lor& x=-\sqrt[6]{{{1}\over{2}}} \\
&&\phantom{xxx}\blue{\text{beide kanten }6 \text{-de machtswortel genomen}}\\
x=\frac{1}{2}\sqrt[6]{32} &\lor& x=-\frac{1}{2}\sqrt[6]{32}\\
&&\phantom{xxx}\blue{\text{vereenvoudigd}} \end{array}#
Ontgrendel volledige toegang


Toegang voor leraar
Vraag een demo account aan. Wij helpen je graag op weg met onze digitale leeromgeving.
Toegang voor student
Is jouw universiteit niet aangesloten?
Via Pass Your Math kan je toegang krijgen tot onze cursussen onafhankelijk van je onderwijsinstelling. Bekijk de prijzen en nog veel meer. Of ga naar
omptest.org als je een OMPT examen moet maken.
omptest.org als je een OMPT examen moet maken.



