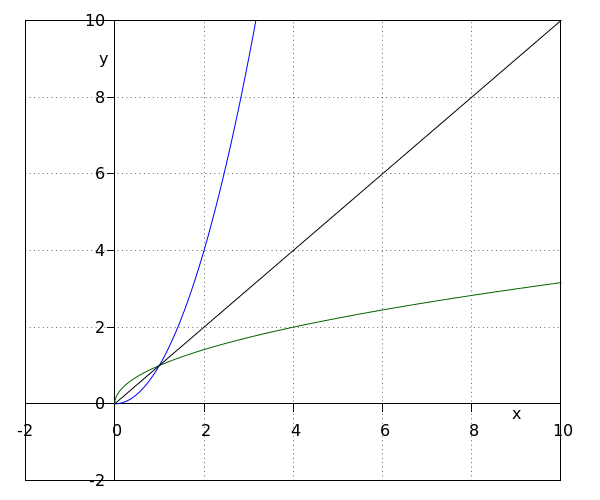
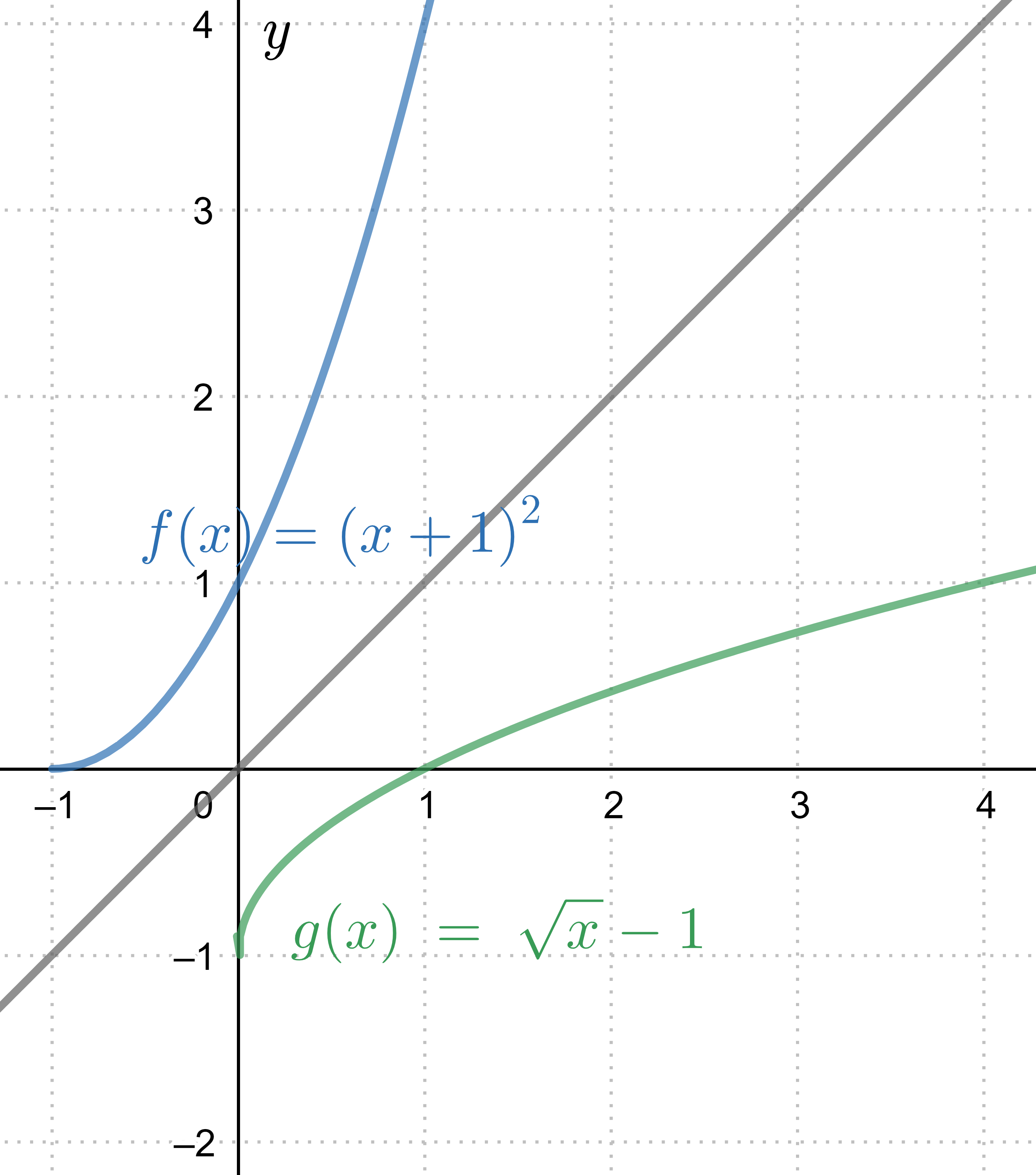We bekijken de functies #\blue{f(x)}=\blue{x^2}# (doorgetrokken) en #\green{g(x)}=\green{\sqrt{x}}# (gestreept) op het domein #\ivco{0}{\infty}#.
Voor deze functies geldt #\blue f(\green{g(x)})=\left(\green{\sqrt{x}}\right)^\blue2=x# voor alle #x# in #\ivco{0}{\infty}#.
Daarom noemen we #\green{g(x)}# de inverse van #\blue{f(x)}#.
Er geldt ook #\green g(\blue{f(x)})=\green{\sqrt{\blue{x^2}}}=x# voor alle #x# in #\ivco{0}{\infty}#.
Daarom noemen we #\blue{f(x)}# de inverse van #\green{g(x)}#.
De functie #\blue{f(x)}# heeft inverse functie #\green{g(x)}# als \[\blue f(\green{g(x)})=x\] voor alle #\green{g(x)}# in het domein van #\blue f#.
Meetkundig gezien is de grafiek van de inverse #\green{g(x)}# het spiegelbeeld van #\blue{f(x)}# in de lijn #y=x#.
We noteren de inverse van #\blue{f(x)}# ook wel met #\green{f^{-1}(x)}#.
Bij het bepalen van de inverse is het domein van de functie belangrijk. Het domein van #\blue{f(x)}# is het bereik van #\green{g(x)}# en het domein van #\green{g(x)}# is het bereik van #\blue{f(x)}#. Dit betekent dat de inverse functie #\green{g(x)}# gedefinieerd is op het bereik van de functie #\blue{f(x)}#.
Voorbeeld
In de afbeelding #\blue{f(x)}=\blue{(x+1)^2}# op het domein #x \ge -1# en zijn inverse #\green{g(x)}=\green{\sqrt{x}-1}# op het domein #x \ge 0#
De functie #\blue{f(x)}=\blue{(x+1)^2}# heeft als domein alle getallen en als bereik alle niet-negatieve getallen. De inverse functie #\green{g(x)}=\green{\sqrt{x}-1}# heeft dus als domein alleen niet-negatieve getallen. Het bereik van #\green{g(x)}# bestaat ook alleen uit de niet-negatieve getallen. De functie #\blue{f(x)}=\blue{(x+1)^2}# heeft dus alleen een inverse op het domein van alle niet-negatieve getallen.
Andersom geldt ook dat de functie #\green{g(x)}=\green{\sqrt{x}-1}# de functie #\blue{f(x)}=\blue{(x+1)^2}# als inverse heeft, maar alleen op het domein van alle getallen groter dan of gelijk aan #-1#. Want dat is het bereik van #\green{g(x)}# en dat is dus het domein van #\blue{f(x)}#.
We zullen deze beperkingen in het domein meestal niet noemen bij het bepalen van de inverse functie, maar impliciet aannemen.
| |
Stappenplan
We bepalen de inverse functie #\green{f^{-1}(x)}# van de functie #\blue{f(x)}#.
|
Voorbeeld
#\blue{f(x)}=\left(x-4\right)^2#.
|
| Stap 1 |
Schrijf de functie als formule, dus in de vorm #y=\ldots#.
|
#y=\left(x-4\right)^2# |
| Stap 2 |
Maak de variabele #x# vrij in de formule #y=\ldots#. Dat betekent dat we de formule schrijven als #x=\ldots#.
|
#x=\sqrt{y}+4# |
| Stap 3 |
Maak in de formule van #y# een #x# en van de #x# een #y#.
|
#y=\sqrt{x}+4# |
| Stap 4 |
Vervang #y# door #\green{f^{-1}(x)}#.
|
#\green{f^{-1}(x)}=\sqrt{x}+4# |
We werken stap 2 uit het voorbeeld uit. Daar willen we de variabele #x# vrijmaken in de formule #y=\left(x-4\right)^2#. Dit gaat door middel van herleiding.
\[\begin{array}{rcl}y&=&\left(x-4\right)^2 \\ &&\phantom{xxx}\blue{\text{oorspronkelijke formule}} \\ \sqrt{y}&=&x-4 \\ &&\phantom{xxx}\blue{\text{beide zijden wortelgetrokken}} \\ \sqrt{y}+4&=&x \\ &&\phantom{xxx}\blue{\text{beide zijden plus }4}\end{array}\]
Dus #x=\sqrt{y}+4#.
Merk op dat het vrij maken van een variabele dus eigenlijk dezelfde vraag is als het bepalen van de inverse functie.
In dat geval hoeven we stap 3 en 4 niet meer uit te voeren en zijn we dus bij stap 2 van het stappenplan klaar.
In stap 2 hebben we aan beide zijden wortelgetrokken om #x# uit het kwadraat vrij te kunnen maken. We nemen dan de positieve wortel. Bij de introductie van de wortelfunctie hebben we immers gezien dat de wortel van een niet-negatief getal een niet-negatief getal is.
Als er een specifiek domein gegeven is, kan het gebeuren dat de inverse functie juist de negatieve wortel heeft. In het voorbeeld heeft #\blue{f(x)}# als domein alle reële getallen en als bereik alle niet-negatieve getallen. De inverse functie #\green{f^{-1}(x)}# heeft als domein alle niet-negatieve getallen en als bereik alle getallen groter of gelijk aan #4#. Dus #\blue{f(x)} =\blue{ (x-4)^2}# heeft alleen op het domein #x \ge 4# de inverse #\green{f^{-1}(x) }= \green{\sqrt{x}+4}#.
Als gevraagd was de inverse van #\blue{f(x)}# te bepalen op het domein #x\le 4# dan hadden we in stap 2 de negatieve wortel moeten nemen. De inverse van #\blue{f(x)} =\blue{ (x-4)^2}# op het domein #x \le 4# is #\green{f^{-1}(x)} = \green{-\sqrt{x}+4}#. Deze functie heeft als domein alle niet-negatieve getallen en als bereik alle getallen kleiner of gelijk aan #4#, wat overeenkomt met het gegeven domein.
Maak #x# vrij in
\[y=\sqrt{x-5}\]
Geef je antwoord in de vorm #x = ...#
#x=y^2+5#
#\begin{array}{rcl}
y&=&\sqrt{x-5} \\ &&\phantom{xxx}\blue{\text{de oorspronkelijke functie}}\\
y^2&=& x-5 \\ &&\phantom{xxx}\blue{\text{beide kanten gekwadrateerd}}\\
y^2+5&=&x \\ &&\phantom{xxx}\blue{\text{beide kanten min }-5}\\
x&=&y^2+5 \\ &&\phantom{xxx}\blue{\text{links en rechts omgewisseld}}\\
\end{array}#
 Inverse functie
Inverse functie