Transformations des fonctions puissances à exposants négatifs

Fonctions: Fonctions rationnelles

Transformations des fonctions puissances à exposants négatifs

Nous avons étudié le graphe d'une fonction irrationnelle $f(x)=\tfrac{1}{x^n}$ où $n \gt 0$ et $n$ est un entier. Tout comme les fonctions puissances de la forme $y=x^n$ où $n \gt 0$ et $n$ est un entier, nous pouvons transformer les fonctions irrationnelles.

Nous pouvons transformer la fonction $f(x)=\frac{1}{x^n}$ de trois manières différentes.

	Transformations	Exemples
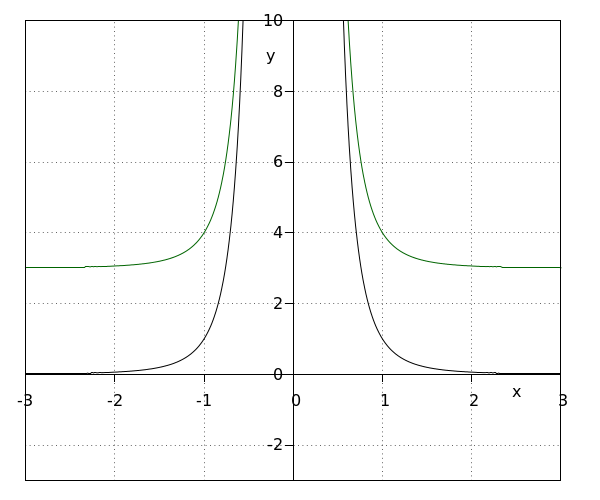
1	Nous déplaçons le graphe de $f(x)=\tfrac{1}{x^n}$ de $\green q$ unités vers le haut. La nouvelle fonction est $f(x)=\frac{1}{x^n}+\green q$ Comme le graphe de la nouvelle fonction est déplacé de $\green q$ unités vers le haut, l'ensemble image devient égal à $\ivoo{\green q}{\infty}$ pour $n$ pair. Si $n$ est impair, l'ensemble image correspond à l'ensemble de tous les nombres différents de $\green q$ . Le domaine reste le même. Ainsi, l'asymptote horizontale est égale à $y=\green q$ et l'asymptote verticale est égale à $x=0$ .	déplacer $f(x)=\frac{1}{x^4}$ de $\green3$ unités vers le haut donne $f(x)=\frac{1}{x^4}+\green3$
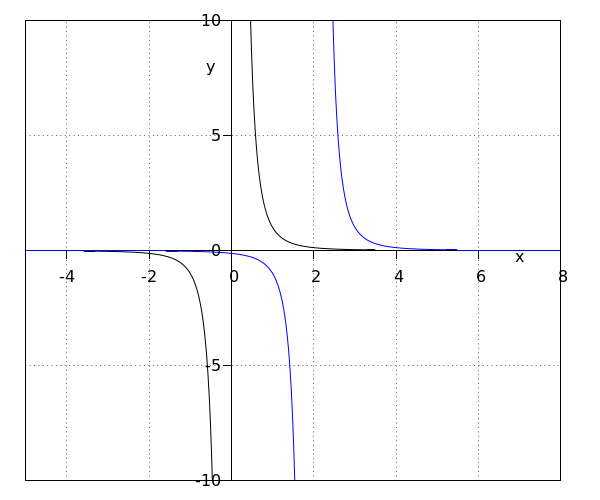
2	Nous déplaçons le graphe de $f(x)=\tfrac{1}{x^n}$ de $\blue p$ unités vers la droite. La nouvelle fonction devient $f(x)=\frac{1}{\left(x-\blue p\right)^n}$ Comme le graphe de la nouvelle fonction est déplacé de $\blue p$ unités vers la droite, le domaine correspond à l'ensemble de tous les nombres différents de $x=\blue p$ . L'ensemble image reste le même. Ainsi, l'asymptote horizontale est égale à $y=0$ et l'asymptote verticale est égale à $x=\blue p$ .	déplacer $f(x)=\frac{1}{x^3}$ de $\blue2$ unités vers la droite donne $f(x)=\frac{1}{\left(x-\blue2\right)^3}$
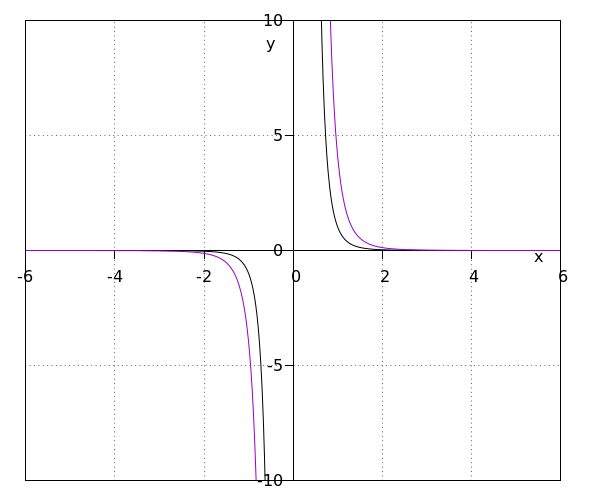
3	Nous étirons le graphe de $f(x)=\tfrac{1}{x^n}$ en multipliant l'expression par $\purple a$ . La nouvelle fonction devient $f(x)=\frac{\purple a}{x^n}$ En multipliant par un nombre positif, le domaine, l'ensemble image et les asymptotes restent inchangés. En multipliant par un nombre négatif, le graphe est inversé. Si $n$ est impair, alors le domaine, l'ensemble image et les asymptotes restent les mêmes. Si $n$ est pair, alors l'ensemble image est également inversé et est $\ivoo{-\infty}{0}$ . Le domaine et les asymptotes restent les mêmes.	multiplication de $f(x)=\frac{1}{x^5}$ par $\purple4$ donne $f(x)=\frac{\purple4}{x^5}$

Plusieurs transformations Nous pouvons également appliquer plusieurs transformations.

Par exemple: Pour $f(x)=\frac{\purple3 }{\left(x-\blue4\right)^4}$ nous déplaçons d'abord le graphe de $\blue4$ unités vers la droite et ensuite nous étirons le graphe obtenu en multipliant les ordonnées des points par $\purple3$ .

En déplaçant le graphe de $\blue p$ unités vers la droite, nous avons pu constater un déplacement de l'asymptote verticale. En particulier, l'axe de symétrie d'une fonction paire est déplacé de $x=\blue p$ unités vers la droite.

Une fonction puissance à exposant négatif pair $n$ admet un centre de symétrie pour $\rv{0,0}$ . En déplaçant le graphe de $\green q$ unités vers le haut, le centre de symétrie est également déplacé de $\green q$ unités vers le haut. De la même manière, en déplaçant le graphe de $\blue p$ unités vers la droite, le centre de symétrie est également déplacé de $\blue p$ unités vers la droite au point $\rv{\blue p, 0}$ .

Considérez les deux graphes ci-dessous.

Le graphe bleu correspond à l'équation:
$y=-{{4}\over{x^6}}$
Quelle est l'équation du graphe vert?

$y=$ $-{{4}\over{\left(x+1\right)^6}}$

Le point $\rv{1,-4}$ appartient au graphe bleu, nous allons étudier où le point correspondant se trouve sur le graphe vert. Sur le graphe vert, ce point correspond à $\rv{0,-4}$ .
Ainsi, le graphe vert est obtenu en déplaçant le graphe bleu de $1$ unités vers la gauche.
Nous remplaçons toutes les occurences de $x$ dans l'expression $y=-{{4}\over{x^6}}$ du graphe bleu par $x+1$ . Cela nous donne l'équation suivante du graphe vert:
$y=-{{4}\over{\left(x+1\right)^6}}$

Nouveau exemple