Trigonometric functions

Trigonometry: Trigonometric functions

Trigonometric functions

The sine, cosine and tangent are not only used at angles, but can also be used as a function.

Sine function

The sine function $f(x)=\sin(x)$ is the function that adds the sine of $x$ to each number $x$ .

$2 \pi$ . $\blue{\text{period}}$ $2 \pi$ .

The function also has an $\green{\text{equilibrium}}$ . This is the middle of the function, or the $y$ -value that lies exactly between the highest and the lowest point. For the sine function, this is $0$ .

Finally, the $\purple{\text{amplitude}}$ of the function is equal to $1$ . This means that the value between the equilibrium and the highest point (or the lowest point) equals $1$ .

In words At Angles in radians we saw that the sine of an angle $\alpha$ is defined as the $y$ -coordinate of the point on the unit circle corresponding with the angle $\alpha$ .

We now interpret the sine as a function. To a value $x$ it assigns the value of the sine of the angle of $x$ radians. This means we get a periodic function, with the angle on the $x$ -axis.

Summarized: the sine function has the angle in radians on the $x$ axis, and the $y$ -coordinate of the corresponding point on the unit circle on the $y$ -axis.

Cosine function

The cosine function $f(x)=\cos(x)$ is the function that adds the cosine of $x$ radians to each number $x$ .

This too has $\blue{\text{period}}$ $2\pi$ .

The $\green{\text{equilibrium}}$ is equal to $0$ .

Additionally, the $\purple{\text{amplitude}}$ of the function is equal to $1$ .

. When we move the cosine function to the right by $\frac{\pi}{2}$ , we have the sine function.

In words At Angles in radians we saw that the cosine of an angle $\alpha$ is defined as the $x$ -coordinate of the point on the unit circle corresponding with the angle $\alpha$ .

We now interpret the cosine as a function. To a value $x$ it assigns the value of the cosine of the angle of $x$ radians. This means we get a periodic function, with the angle on the $x$ -axis.

Summarized: the cosine function has the angle in radians on the $x$ axis, and the $x$ -coordinate of the corresponding point on the unit circle on the $y$ -axis.

Tangent function

The tangent function $f(x)=\tan(x)$ is the function that adds the tangent of $x$ radians to each number $x$ .

. The $\blue{\text{period}}$ is equal to $\pi$ .

The vertical asymptotes of the tangent function are $x=\frac{\pi}{2}+k \cdot \pi$ , in which $k$ is an integer, as for the $x$ -values $\frac{\pi}{2}$ , $\frac{3 \pi}{2}$ and $\frac{5 \pi}{2}$ , but also for $\frac{-3 \pi}{2}$ .

Consider the graph below.

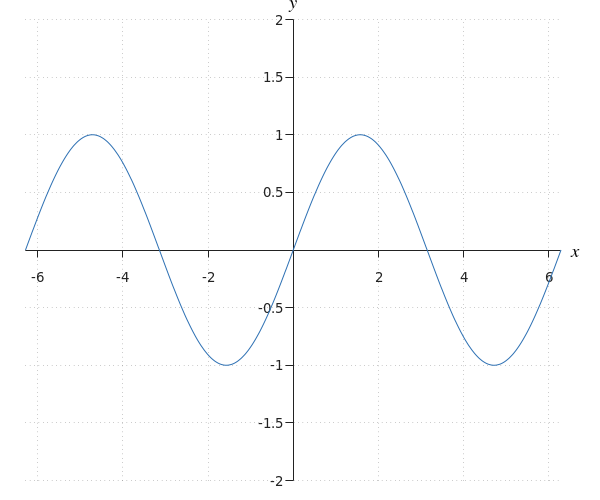
To which function does this graph belong?

$f(x)=\tan \left(x\right)$

We see a function with period $\pi$ and vertical asymptotes $x=\tfrac{\pi}{2}$ , $x=\tfrac{3 \pi}{2}$ , $x=-\tfrac{\pi}{2}$ and $x=-\tfrac{3 \pi}{2}$ . This means the function is equal to $f(x)=\tan \left(x\right)$ .

New example