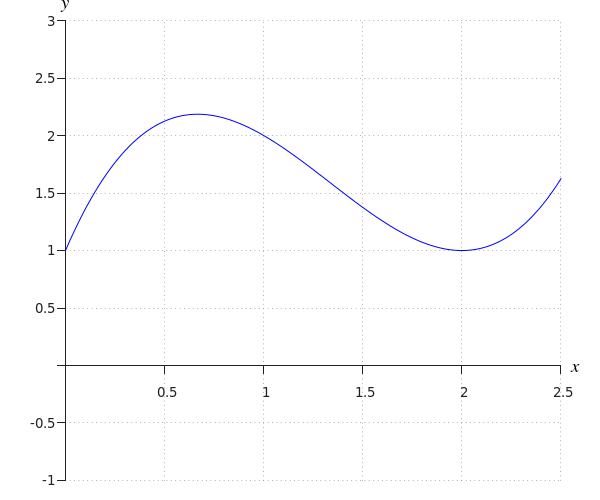
De hoogste waarde van een deel van een grafiek noemen we een lokaal maximum.
De kleinste waarde van een deel van een grafiek noemen we een lokaal minimum.
Beide zijn extreme waarden van een functie.
Indien we een functie bekijken op een beperkt domein kunnen de waarden op de grenzen van het domein ook een lokaal maxima of minima zijn en dus een extreme waarde.
Als we kijken naar de functie #f(x)=x^2# op het domein #\ivcc{2}{5}# hebben we een lokaal minimum in #x=2# en een lokaal maximum in #x=5#. Als we #x^2# op de hele getallenlijn bekijken hebben we enkel een lokaal minimum, voor #x=0#.
Tot nu toe hebben we in deze cursus vaak specifiek naar de #x#-waarden van bijzondere punten gekeken, maar de maxima en de minima zijn de #y#-waarden van deze punten.
Dus in het voorbeeld is een lokaal maximum van de groene grafiek #3.5# en #\red{\text{niet}}# #0#. Een lokaal minimum van de blauwe grafiek is #0.5# en #\red{\text{niet}}# #0#.
We hebben gezien dat de lokale maxima en minima het hoogste punt op een deel van de grafiek zijn. De globale maxima en minima zijn het hoogste punt van de hele grafiek.
In het voorbeeld van de groene grafiek is het lokale maximum ook globaal. Net zo is in de blauwe grafiek het lokale minimum ook globaal. Dit is lang niet altijd het geval.
Ook als er lokale maxima en minima zijn hoeft er niet altijd een globaal maximum of minimum te zijn.
We kunnen met behulp van de afgeleide eenvoudig de extreme waardes van een functie berekenen.
Als een functie #\blue{f(x)}# een lokaal maximum of minimum heeft in #x=\orange{c}#, dan #\green{f'(\orange{c})}=0#.
Voorbeeld
\[\begin{array}{rcl}\blue{f(x)}&=&\blue{x^2}\\ \green{f'(x)}&=&\green{2x}\\ \green{f'(\orange{0})}&=&0\end{array}\]
De functie moet in punt #x=\orange{c}# ook differentieerbaar zijn. In deze cursus zullen we geen functies bekijken die niet differentieerbaar zijn, maar in de praktijk kan dat wel voorkomen.
Dat de afgeleide in een extreme waarde gelijk is aan #0# komt overeen met zeggen dat de raaklijn in het punt horizontaal is. In het plaatje hieronder zien we dit ook terug.
Deze stelling geldt niet als #c# een grenswaarde van het domein van de functie is. Als we #f(x)=x^2# bekijken op het domein #\ivcc{2}{5}# zijn #2# en #5# duidelijk extreme waarden, maar is de afgeleide niet gelijk aan #0#.
Als de afgeleide #\green{f'(x)}# van een functie #\blue{f(x)}# gelijk is aan #0# in een punt #\orange{c}# betekent dit niet per definitie dat er in het punt #\orange{c}# een extreme waarde is. De afgeleide van #\blue{f(x)=x^3}# is gelijk aan #0# in het punt #\orange{0}#, maar deze heeft hier geen extreme waarde.
| |
Stappenplan
|
Voorbeeld
|
| |
Bepaal de extreme waarden van een functie #f(x)#. Bepaal voor elke extreme waarde of het een lokaal minimum, lokaal maximum is of geen van beiden.
|
#\qqquad \begin{array}{rcl}f(x)\phantom{'}&=&x^4-2x^2\end{array}#
|
| Stap 1 |
Bereken de afgeleide #f'(x)#.
|
#\qqquad \begin{array}{rcl}f'(x)&=&4x^3-4x\end{array}#
|
| Stap 2 |
Los #f'(x)=0# op om #x#-coördinaten te vinden van de punten die mogelijk een extreme waarde zijn.
|
#\qqquad \begin{array}{rcl} 4x^3-4x&=&0\\ x&=&0 \lor 4x^2-4=0\\ x&=&0\lor x^2=1\\ \green{x}&\green{=}&\green{0} \lor \blue{x=-1} \lor\orange{x=1}\end{array}#
|
| Stap 3 |
Schets de grafiek om erachter te komen welke punten een lokaal maximum zijn en welke punten een lokaal minimum (en welke punten eventueel geen maximum of minimum) zijn.
|
|
| Stap 4 |
Substitueer de gevonden #x#-coördinaten in #f(x)# en bepaal zo de extreme waarden.
|
#f(\blue{-1})=-1#,
#f(\orange{1})=-1#,
#f(\green{0})=0#
Dus lokaal minimum is #-1# en
lokaal maximum is #0#
|
Het berekenen van lokale minima of maxima is iets wat een grote rol speelt in optimalisatieproblemen. Men schrijft dan een probleem om naar de vorm van een functie, en bepaalt dan naar wens het maximum of minimum.
We geven een zeer eenvoudig voorbeeld. Stel een boer heeft #500# meter aan gaas gekocht om een rechthoekig gebied te omheinen, en wilt de oppervlakte van dit omheinde gebied zo groot mogelijk hebben, wat zijn dan de beste afmetingen? Als eerst merken we op dat het oppervlakte van dit gebied gegeven wordt door #O=x\cdot y#, waar we #x# voor de breedte en #y# voor de hoogte schrijven, #O# betekent de oppervlakte. We hebben #500# meter aan gaas, wat verdeeld moet worden over de lengte en de breedte. Er geldt dus #2x+2y=500#. Omschrijven geeft \[y=250-x\] We vullen dit in in de formule voor de oppervlakte, en krijgen \[O=x\cdot(250-x)=250\cdot x - x^2\] Dit is de formule die we willen maximaliseren. Het volgen van het stappenplan geeft #x=125#. Dit betekent dat het voor de boer het verstandigst is om een perfect vierkant gebied te omheinen.
Vaak zijn de functies die gemaximaliseerd of geminimaliseerd moeten worden veel ingewikkeldere functies, met veel meer variabelen. We zullen hier niet op in gaan.
We kunnen als alternatief voor stap #3# gebruik maken van een tekenschema. Uit stap #2# vinden we de nulpunten #x_1,\ldots, x_n# van #f'(x)#. In de intervallen tussen deze nulpunten van de afgeleide, zoals #\ivoo{x_i}{x_{i+1}}#, zitten nu geen nulpunten. We kunnen nu concluderen dat óf de waarden van #f'(x)# voor iedere #x# in het interval positief zijn, of allemaal negatief zijn. Als we dus één punt uit het interval invullen in #f'(x)# weten we gelijk het teken van het gehele interval: positief of negatief. In het tekenschema schrijven we de intervallen op met het bijbehorende teken.
| Interval |
#\ivoo{-\infty}{x_1}# |
#x_1# |
#\ivoo{x_1}{x_2}# |
#x_2# |
#\ldots# |
#x_n# |
#\ivoo{x_n}{\infty}# |
| Teken |
#+# of #-# |
#0# |
#+# of #-# |
#0# |
#\ldots# |
#0# |
#+# of #-# |
Aan de hand van dit tekenschema kunnen we bepalen of een punt #x_i# de #x# waarde van een lokaal maximum, minimum of geen van beide is. We doen dit aan de hand van de tekens van #\ivoo{x_{i-1}}{x_i}# en #\ivoo{x_i}{x_{i+1}}#.
- Als het teken van #\ivoo{x_{i-1}}{x_i}# positief is, en dat van #\ivoo{x_i}{x_{i+1}}# negatief, dan is #x_i# de #x#-coördinaat van een lokaal maximum.
- Als het teken van #\ivoo{x_{i-1}}{x_i}# negatief is, en dat van #\ivoo{x_i}{x_{i+1}}# positief, dan is #x_i# de #x#-coördinaat van een lokaal minimum.
- Als het teken van #\ivoo{x_{i-1}}{x_i}# positief is, en dat van #\ivoo{x_i}{x_{i+1}}# ook positief, dan is #x_i# niet de #x#-coördinaat van een extreme waarde.
- Als het teken van #\ivoo{x_{i-1}}{x_i}# negatief is, en dat van #\ivoo{x_i}{x_{i+1}}# ook negatief, dan is #x_i# niet de #x#-coördinaat van een extreme waarde.
In het voorbeeld vonden we de nulpunten #x_1=-1, x_2=0# en #x_3=1#. We krijgen het volgende tekenschema
| Interval |
#\ivoo{-\infty}{-1}# |
#-1# |
#\ivoo{-1}{0}# |
#0# |
#\ivoo{0}{1}# |
#1# |
#\ivoo{1}{\infty}# |
| Teken |
#-# |
#0# |
#+# |
#0# |
#-# |
#0# |
#+# |
We zien dat #x=-1# en #x=1# beide een lokaal minimum geven, en dat #x=0# een lokaal maximum geeft.
Geef de twee waarden van #x# waar de functie #f# gegeven door \[f(x)=x^3-4x^2+4x+1\] een extreme waarde (lokaal maximum of minimum) heeft.
De kleinste waarde van #x# wordt met #x_-# aangegeven en de grootste waarde met #x_+#. Geef je antwoorden als een onvereenvoudigbare breuk.
#x_-=# #{{2}\over{3}}# en #x_+=# #2#
| Stap 1 |
We bepalen de afgeleide van #f(x)=x^3-4x^2+4x+1#. Deze is gelijk aan:
\[f'(x)=3x^2-8x+4\] |
| Stap 2 |
We bepalen de #x#-coördinaten van de mogelijke extreme waarden door de afgeleide gelijk aan #0# te stellen en de vergelijking op te lossen.
\[\begin{array}{rcl}3x^2-8x+4&=&0 \\ &&\phantom{xxx}\blue{\text{de op te lossen vergelijking}}\\
x=\frac{8-\sqrt{(-8)^2-4\cdot 3\cdot 4}}{2\cdot 3} &\lor& x=\frac{8+\sqrt{(-8)^2-4\cdot 3\cdot 4}}{2\cdot 3} \\ &&\phantom{xxx}\blue{\text{abc-formule}}\\
x=\frac{8-\sqrt{16}}{6} &\lor& x=\frac{8+\sqrt{16}}{6} \\ &&\phantom{xxx}\blue{\text{vereenvoudigd}}\\
x=\frac{8-4}{6} &\lor& x=\frac{8+4}{6} \\ &&\phantom{xxx}\blue{\text{vereenvoudigd}}\\
x={{2}\over{3}} &\lor& x=2 \\ &&\phantom{xxx}\blue{\text{vereenvoudigd}}\end{array}\] |
| Stap 3 |
We tekenen de grafiek van #f(x)#.
Dus er ligt een lokaal maximum bij #x={{2}\over{3}}# en een lokaal minimum bij #x=2#. Dus beide gevonden #x#-waarden horen bij een extreme waarde.
Dus #x_-={{2}\over{3}}# en #x_+=2# |
 Extreme waarden
Extreme waarden