Differentiaalvergelijkingen: Richtingsvelden en oplossingskrommen
De methode van Euler
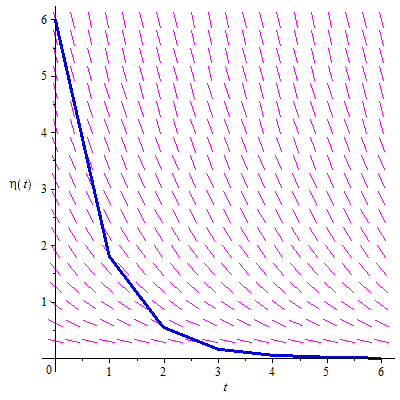
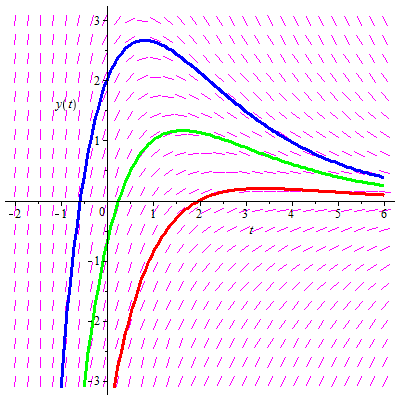
Als er voor een expliciet eerste-orde dynamisch systeem geen exacte oplossing (in termen van bekende functies) voorhanden is, of als een eerste oriëntatie van het gedrag van het systeem gewenst is, dan biedt de meetkundige aanpak met het richtingsveld uitkomst. Door de lijnelementen van het richtingsveld te volgen vinden we een benadering van de oplossingskromme met gegeven beginvoorwaarde door middel van lijnstukjes.
De methode van Euler
Bekijk het dynamisch systeem van de vorm \[\frac{\dd y}{\dd t}=\varphi(t,y)\] waarbij #\varphi# een continue functie van twee variabelen is.
Laat #\delta# een klein positief getal zijn. Een numerieke benadering van de oplossingskromme van het dynamisch systeem met beginvoorwaarde #y(t_0)=\eta_0# wordt gegeven door de iteratieve formule \[\eta_{k+1}=\eta_k+\varphi(t_k,\eta_k)\cdot \delta\] waarbij de punten \(t_k\) zó gekozen zijn dat elk tweetal een opeenvolgende onderlinge afstand \(\delta\) heeft, zodat: \[t_k=t_0+k\cdot \delta \] voor \(k=0,1,2,\ldots,n\).
Deze aanpak heet de methode van Euler en het getal \(\delta\) heet de stapgrootte.
We beginnen met \(\eta_0=y_0\) op tijdstip \(t_0\) en bepalen de benadering \(\eta_1\) van \(y(t_1)\) door de raaklijn in het punt \(\rv{t_0,\eta_0}\) te gebruiken als benadering voor de grafiek van de oplossing \(y\) op het segment \([t_0,t_1]\): \[ \eta_1=\eta_0+\varphi(t_0,\eta_0)\cdot \delta \] Uitgaande van het nu bekende punt \(\rv{t_1,\eta_1}\) benaderen we de volgende functiewaarde \(y(t_2)\) met \[\eta_2=\eta_1+\varphi(t_1,\eta_1)\cdot \delta\] Enzovoorts. Dit benaderingsproces leidt tot de algemene formule voor \(\eta_{k+1}\).
In onderstaande figuur is het richtingsveld getekend van het dynamisch systeem\[\frac{\dd y}{\dd t}=-0.7y\] tezamen met de benadering van de oplossingskromme, berekend volgens de methode van Euler met stapgrootte \(\delta =1\) en beginvoorwaarde \( y(0)=6\). Naarmate de stapgrootte \(\delta \) kleiner is, wordt de grafiek van de berekende functiewaarden gladder en begint deze steeds meer op de grafiek van een exacte oplossing te lijken.
De formule \(\eta_{k+1}=\eta_k+\varphi(t_k,\eta_k)\cdot \delta\) is in dit specifieke geval gelijk aan \[\eta_{k+1}=\eta_k-0.7\cdot \eta_k\cdot \delta=\eta_k\cdot 0.3\cdot \delta=\eta_0\cdot(0.3\cdot \delta)^{k+1}=6\cdot(0.3\cdot \delta)^{k+1}\] De exacte oplossing van dit beginwaardeprobleem is \(y(t)=6\e^{-0.7t}\)
Als in de Eulermethode een negatieve tijdstap \(\delta\) gebruikt wordt, kunnen voorafgaande waarden in een integraalkromme berekend worden. De Eulermethode is dus geschikt om integraalkrommen die door een zeker punt gaan, uit te rekenen in zowel de richting van het verleden als van de toekomst.
In onderstaande figuur zijn de integraalkrommen van de GDV \[\frac{\dd y}{\dd t}=3\e^{-t}-\tfrac{1}{2}y,\] getekend door de punten \(\rv{2,0},\;\rv{1,1},\;\rv{0,2}\)
De groene integraalkromme heeft de gangbare vorm van het concentratieverloop van een oraal toegediend medicijn. Later zullen we zien dat dit farmacokinetische model ook exact oplosbaar is en oplossingskrommen van deze vorm heeft.
Er zijn talloze algoritmen voor het numeriek oplossen van differentiaalvergelijkingen; deze vallen buiten het bestek van deze cursus. De belangrijkste boodschap is dat er dergelijke numerieke oplossingsmethoden bestaan en dat deze nuttig zijn om inzicht in oplossingen van de GDV te verkrijgen.
Om de uitvoering van de methode van Euler zelf te ervaren wordt hieronder een interactieve versie gepresenteerd.
Maak het aantal stappen #s# groter om een versie met kleinere stappen te zien, en voer eventueel andere rechterleden voor de differentiaalvergelijking in het veld achter "#\dd y/\dd t =#". Druk op de update knop om het resultaat te zien.
omptest.org als je een OMPT examen moet maken.
