Hoofdstuk 1: Beschrijvende statistiek: Variabiliteit
 Spreidingsbreedte, interkwartielafstand, en de vijf-getallensamenvatting
Spreidingsbreedte, interkwartielafstand, en de vijf-getallensamenvatting
De variabiliteit of spreiding van een verdeling meet de mate waarin de scores onderling van elkaar verschillen. Als het onderlinge verschil tussen de scores over het algemeen klein is, dan spreken we van een verdeling met een lage variabiliteit. Zijn er daarentegen grote onderlinge verschillen, dan spreken we van een verdeling met een hoge variabiliteit.
De simpelste manier om de variabiliteit van een verdeling te bepalen is het berekenen van de spreidingsbreedte.
Spreidingsbreedte
Definitie
De spreidingsbreedte is het verschil tussen de hoogste en de laagste score van een verdeling.
Formule
\[\text{spreidingsbreedte} = X_{max} - X_{min} \]
Aangezien de spreidingsbreedte de variabiliteit meet op basis van de eindpunten van de verdeling, is de spreidingsbreedte zeer gevoelig voor de aanwezigheid van uitschieters in de dataset.
Een alternatieve maat voor de variabiliteit, die veel minder gevoelig is voor uitschieters, is de interkwartielafstand.
Interkwartielafstand
Definitie
De interkwartielafstand (IKR) is het verschil tussen het eerste en derde kwartiel van een verdeling.
Formule
\[\text{IKR} = Q_3 - Q_1\]
Kwartielen zijn de waarden die een verdeling in vier gelijke delen splitsen, vergelijkbaar met hoe de mediaan een verdeling in twee gelijke delen splitst. De interkwartielafstand meet dus hoe verspreid de middelste #50\%# van de data is. Als gevolg hiervan is de interkwartielafstand volledig onafhankelijk van de kleinste en grootste #25\%# van de scores in de dataset, en dus ongevoelig voor aanwezigheid uitschieters.
Vaak worden de spreidingsbreedte en de interkwartielafstand gecombineerd met de mediaan tot een zogenaamde vijf-getallensamenvatting.
#\phantom{0}#
Vijf-getallensamenvatting
Definitie
De vijf-getallensamenvatting bestaat uit de volgende vijf punten van een verdeling:
- Minimum
- Eerste kwartiel
- Mediaan
- Derde kwartiel
- Maximum
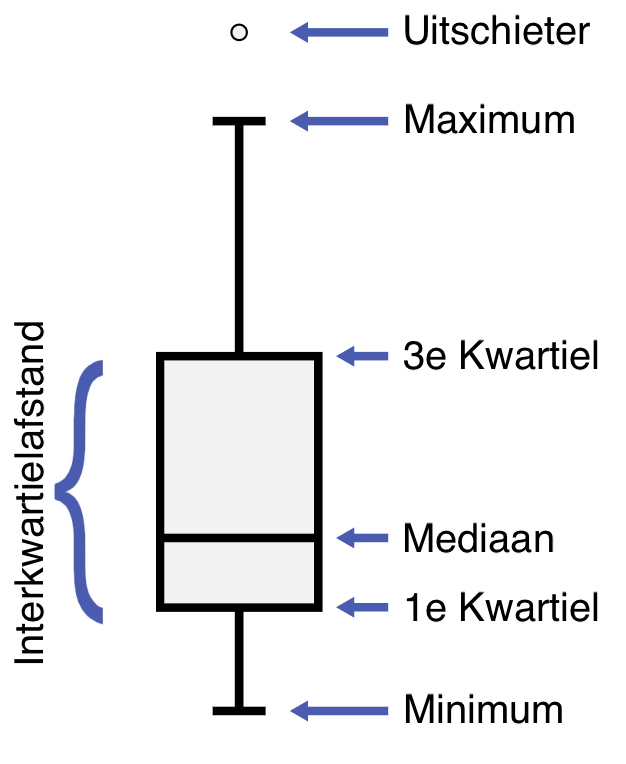
De visuele weergave van de vijf-getallensamenvatting heet een boxplot.
#\phantom{0000000000}# Boxplot

omptest.org als je een OMPT examen moet maken.



