Hoofdstuk 1: Beschrijvende statistiek: Z-Scores
 Z-scores
Z-scores
Eerder in dit hoofdstuk hebben we kwantielen geïntroduceerd als een manier om de locatie van een score ten opzichte van alle andere scores in de verdeling uit te drukken. Zo is bijvoorbeeld het #75^{e}# percentiel van een verdeling de score die groter is dan (of gelijk is aan) #75\%# van alle scores in de verdeling.
Behalve de locatie van een score ten opzichte van alle andere scores, is het ook nuttig om de locatie van een score ten opzichte van het gemiddelde van de verdeling te weten. Op het eerste gezicht zou de afwijking van het gemiddelde in staat moeten zijn om dit doel te dienen. Eén van de tekortkomingen van afwijkingsscores, echter, is dat deze relatief slecht zijn in het beschrijven van de exacte locatie van een score.
Hoewel het teken (#+/-#) van de afwijkingsscore ons kan vertellen aan welke zijde van het gemiddelde de score ligt, is de waarde van een afwijkingsscore geen goede indicatie van hoe ver van het gemiddelde de score ligt.
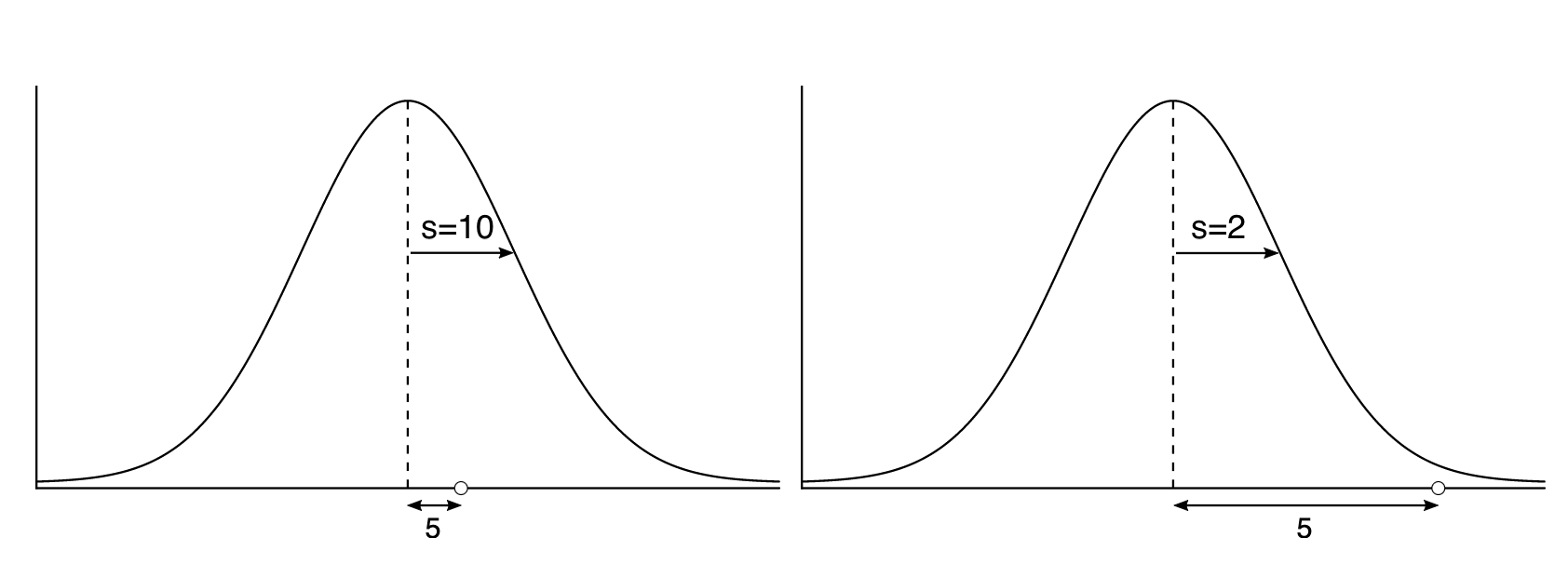
Stel dat we een score hebben die #5# eenheden boven het steekproefgemiddelde ligt. Afhankelijk van de grootte van de spreiding in de verdeling, zou deze score ofwel op een grote afstand danwel op een kleine afstand van het gemiddelde kunnen liggen.
- Als de steekproef een standaardafwijking van #s=10# heeft, dan ligt de score relatief dichtbij het gemiddelde.
- Heeft de steekproef echter een een standaardafwijking van #s=2# heeft, dan bevindt de score zich op behoorlijk grote afstand van het gemiddelde.
Door de afwijking van het gemiddelde te delen door de standaardafwijking van de verdeling, kan een afwijkingsscore omgezet worden in een bruikbare omschrijving van de locatie van een score. Het resultaat van deze transformatie wordt ookwel een #z#-score genoemd.
z-scores
Definitie
Een #z#-score of standaardscore geeft aan hoeveel standaardafwijkingen een score van het gemiddelde ligt.
Formule
\[z = \cfrac{X - \bar{X}}{s}\]
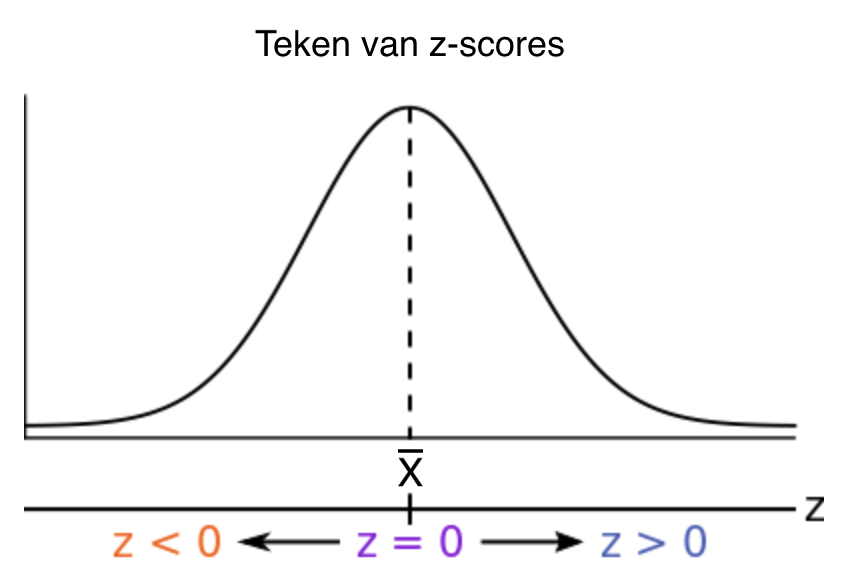
Het teken van een #z#-score draagt dezelfde informatie als het teken van de afwijkingsscore, namelijk aan welke kant van het gemiddelde de score ligt:
- Scores met een #\blue{\text{positieve}}# #z#-score liggen #\blue{\text{boven}}# het gemiddelde.
- Scores met een #\orange{\text{negatieve}}# #z#-score liggen #\orange{\text{onder}}# het gemiddelde.
- Een #z#-score van #\purple{\text{nul}}# geeft aan dat de score #\purple{\text{gelijk is}}# aan het gemiddelde.
In tegenstelling tot de waarde van een afwijkingsscore, is de waarde van de #z#-score wel een goede indicatie van de exacte locatie van een score te opzichte van het gemiddelde, omdat er bij de berekening van #z#-scores rekening gehouden wordt met de grootte van de spreiding in de verdeling.
Hierdoor zijn #z#-scores bijzonder geschikt voor het vergelijken van scores die afkomstig zijn van verschillende verdelingen. Als twee waarnemingen afkomstig van verschillende verdelingen dezelfde #z#-score hebben, dan betekent dit dat beide scores zich relatief op dezelfde afstand van het gemiddelde bevinden.
#z#-scores zijn een maat voor de afwijking van het gemiddelde, uitgedrukt in standaardafwijkingen. Een score die onder het gemiddelde ligt heeft een negatieve #z#-score.
Een score die #2# standaardafwijkingen onder het gemiddelde ligt zal dus een #z#-score van #-2# hebben.

omptest.org als je een OMPT examen moet maken.



