Hoofdstuk 2: Correlatie: Correlatie
 Weergave van de relatie tussen twee variabelen
Weergave van de relatie tussen twee variabelen
Kruistabel
Om de relatie tussen twee categorische/kwalitatieve variabelen te onderzoeken, kunnen we een kruistabel opstellen.
Een kruistabel is vergelijkbaar met een frequentietabel, in de zin dat beide tabellen een overzicht geven van de geobserveerde frequenties in elke meetcategorie. Het verschil tussen de twee tabellen is dat een frequentietabel de frequenties van één enkele variabele weergeeft, terwijl een kruistabel de frequenties van twee variabelen tegen elkaar afzet.
Hieronder is een kruistabel weergeven voor de relatie tussen geslacht en de voorkeur voor een bepaald soort huisdier:
| Voorkeur voor honden | Voorkeur voor katten | Totaal | |
| Man | 25 | 15 | 40 |
| Vrouw | 20 | 40 | 60 |
| Totaal | 45 | 55 | 100 |
Omdat de rijen en kolommen een verschillend aantal waarnemingen bevatten, is het verband tussen de twee variabelen niet onmiddellijk duidelijk. Om een beter begrip van de relatie te krijgen, kunnen we de absolute frequenties in de tabel omzetten naar kolom- of rij percentages:
- Om het kolom percentage van een cel te berekenen, delen we de absolute frequentie in de cel door het bijbehorende kolomtotaal.
- Om het rij percentage van een cel te berekenen, delen we de absolute frequentie in de cel door het bijbehorende rijtotaal.
Als we voor de bovenstaande tabel alle absolute frequenties omzetten in rij percentages, dan levert dit de de volgende tabel op:
| Voorkeur voor honden | Voorkeur voor katten | Totaal | |
| Man | 62,5% | 37,5% | 100% |
| Vrouw | 33,3% | 66,7% | 100% |
| Totaal |
Deze tabel met percentages suggereert dat er inderdaad een relatie bestaat tussen geslacht en de voorkeur voor een bepaald soort huisdier:
- Mannen lijken over het algemeen een voorkeur te hebben voor honden (62,5% versus 37,5%).
- Vrouwen lijken over het algemeen een voorkeur te hebben voor katten (33,3% versus 66,7%).
\[\text{}\]
Spreidingsdiagram
De relatie tussen twee numerieke/kwantitatieve variabelen kan visueel worden weergegeven met behulp van een spreidingsdiagram.
Een spreidingsdiagram is een #X#-#Y# grafiek waarbij één variabele langs elke as wordt uitgezet. Elk puntje in de grafiek stelt een paar waarnemingen voor.
\[\begin{array}{c|c|c}
\text{Student}&\text{Tijd gestudeerd}&\text{Cijfer}\\
\hline
1&5&5.0\\
2&5&6.2\\
3&8&7.1\\
4&9&6.3\\
5&10&6.2\\
6&11&8.1\\
7&11&6.3\\
8&12&7.0\\
9&14&7.5\\
10&16&7.4\\
11&17&9.0\\
12&17&7.6\\
\end{array}\]
#\phantom{0}# 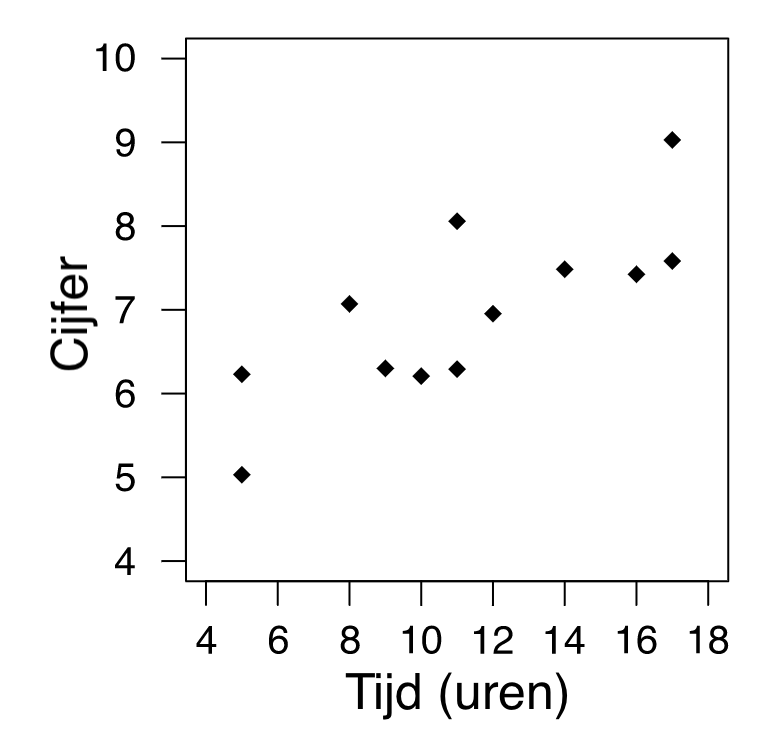
Om een indruk te krijgen van de relatie tussen de twee variabelen, kunnen we een 'wolk' rond de punten in het spreidingsdiagram tekenen.
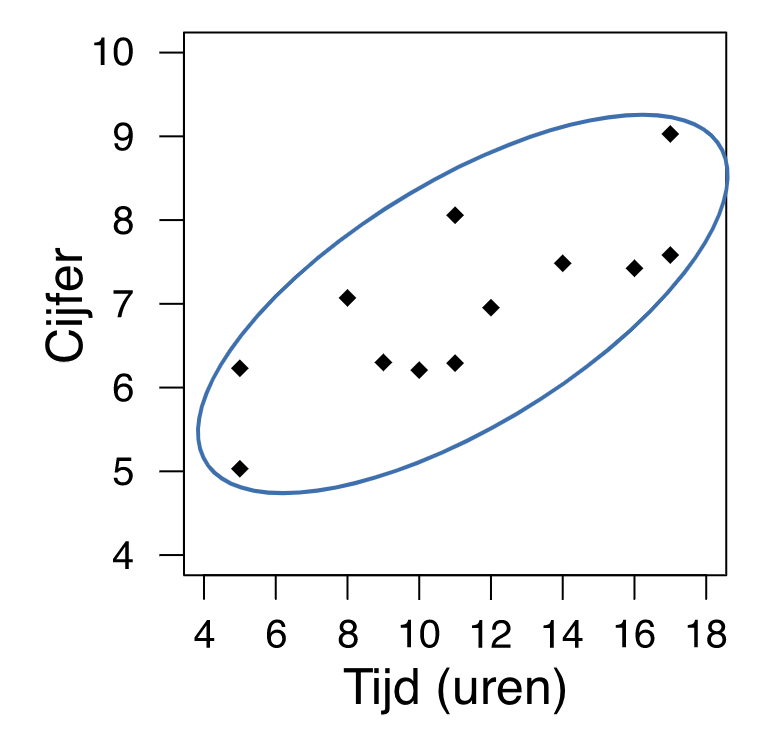
In dit geval heeft de wolk de vorm van een ellips die zich van linksonder naar rechtsboven uitstrekt, wat wat wijst op een positieve lineaire relatie.
Dit suggereert dat studenten die langer studeren over het algemeen ook betere cijfers halen.

omptest.org als je een OMPT examen moet maken.



