Richting
De richting van het verband tussen twee variabelen kan zowel positief als negatief zijn.

Wanneer twee variabelen een positief verband hebben, hebben ze de neiging in dezelfde richting te bewegen. Dit houdt in dat wanneer de waarde van #X# toeneemt, de waarde van #Y# over het algemeen ook toeneemt. Evenzo, als #X# afneemt, dan doet #Y# dit ook.

Wanneer twee variabelen een negatief verband hebben, hebben ze de neiging in tegengestelde richting te bewegen. Dit houdt in dat wanneer de waarde van #X# toeneemt, de waarde van #Y# over het algemeen afneemt. Evenzo, als #X# afneemt, dan neemt #Y# toe.

Vorm
De vorm van een relatie beschrijft het algemene patroon in de data. De twee typen relaties die binnen de statistiek het meest onderzocht worden zijn de lineaire en de monotone relatie.

Een lineaire relatie kan grafisch worden weergegeven als een rechte lijn. Als twee variabelen #X# en #Y# een lineair verband vertonen, dan betekent dit dat als de waarde van #X# met een bepaald percentage veranderd, de waarde van #Y# met hetzelfde percentage verandert.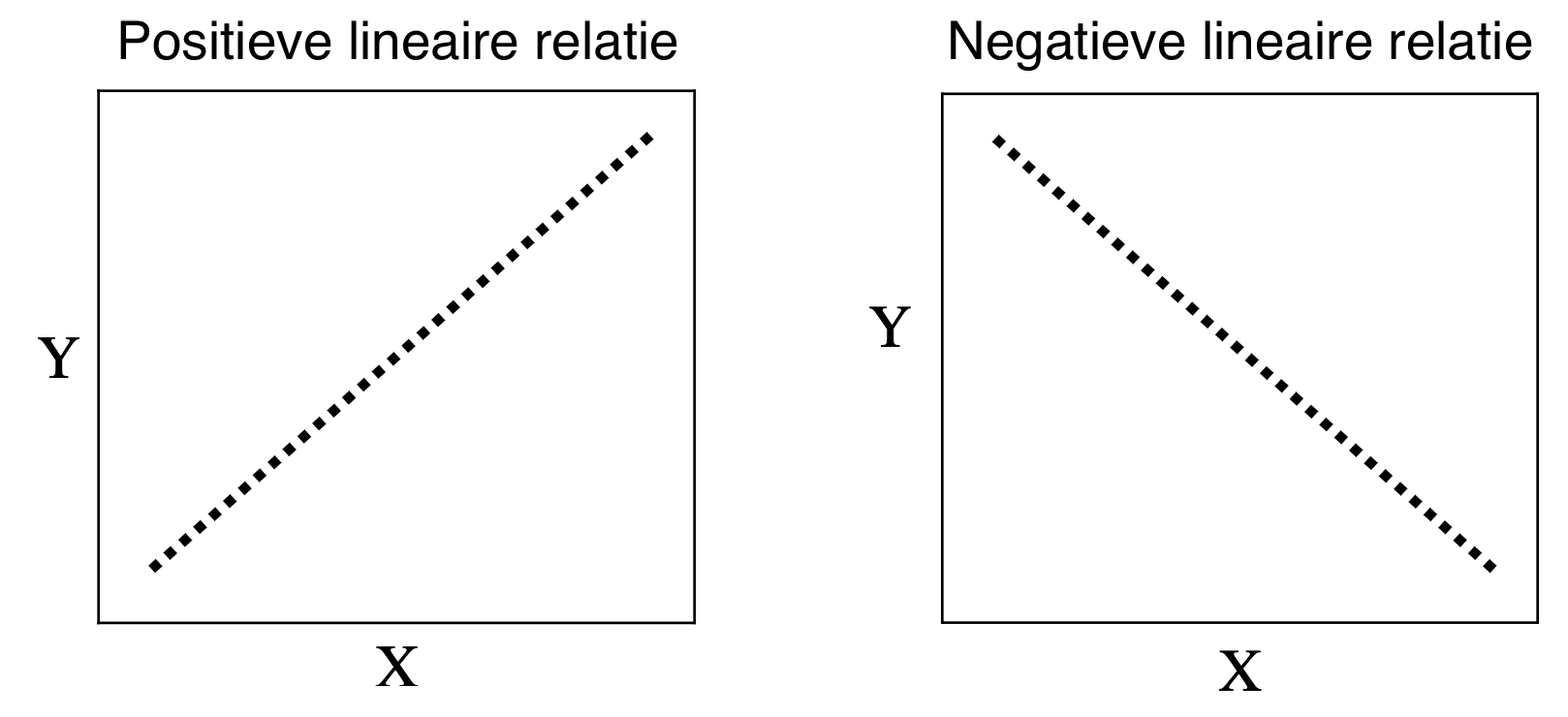


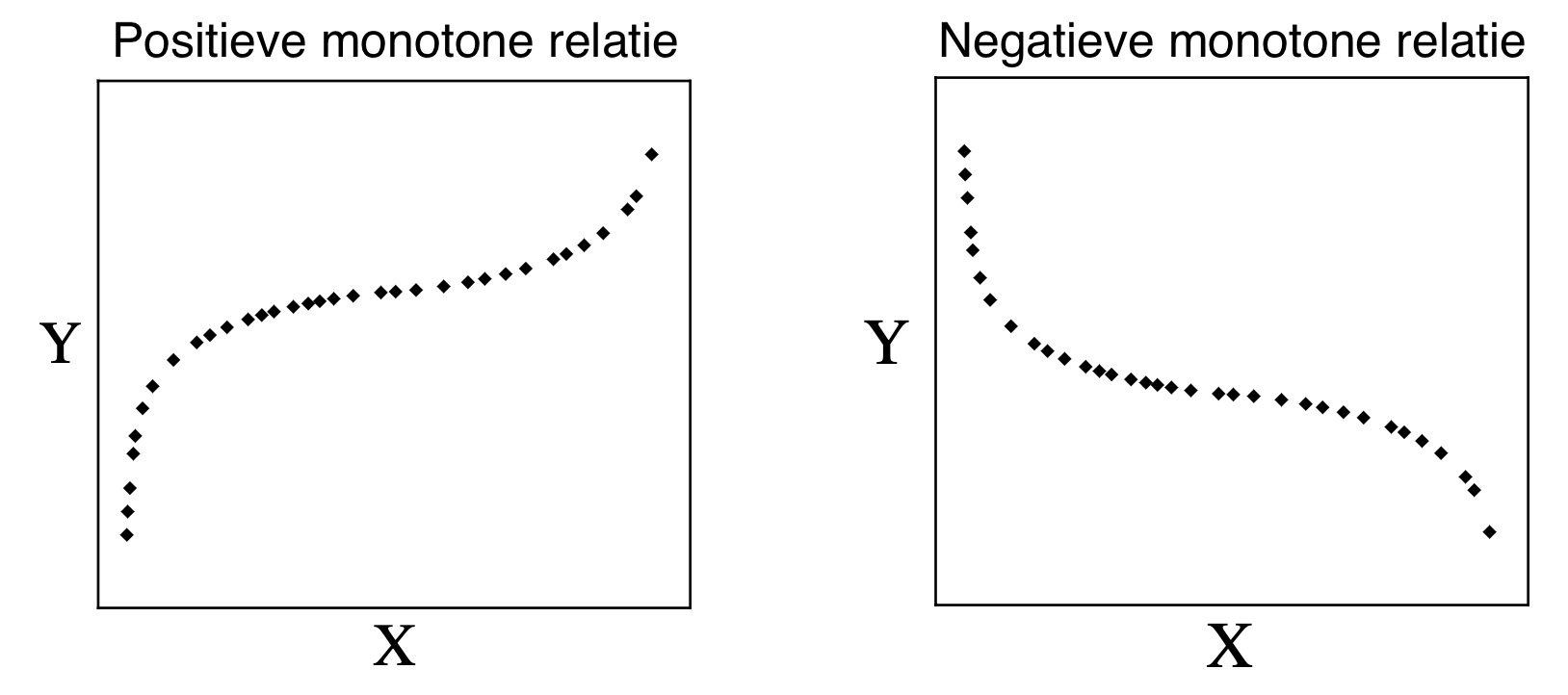
Net als een lineaie relatie, kan een monotone relatie ofwel een positieve of negatieve richting hebben:

• Als twee variabelen een positieve monotone relatie vertonen, dan betekent dit dat als #X# toeneemt, #Y# ofwel toeneemt of constant blijft, maar nooit afneemt.
• Als twee variabelen een negatieve monotone relatie vertonen, dan betekent dit dat als #X# toeneemt, #Y# ofwel afneemt of constant blijft, maar nooit toeneemt.

Kracht
De kracht van het verband tussen twee variabelen wordt bepaald door de grootte van de correlatiecoëfficiënt. Een correlatiecoëfficiënt neemt altijd een waarde aan tussen #-1# en #+1#:

• Een coëfficiënt van #-1# geeft een perfecte negatieve relatie aan.
  
  
• Een coëfficiënt van #+1# geeft een perfecte positieve relatie aan.
  
  
• Een coëfficiënt van #0# geeft aan dat de twee variabelen ongerelateerd zijn.

Voor elk soort relatie (lineair, monotoon, of anders) bestaat een aparte correlatiecoëfficiënt. Het gevolg hiervan is dat het vinden van een coëfficiënt van #0# niet automatisch betekent dat de twee variabelen op geen enkele manier aan elkaar gerelateerd zijn.

Als we bijvoorbeeld een lineaire correlatiecoëfficiënt van #0# vinden, dan zegt dit niks over de sterkte van een eventueel monotoon verband tussen de variabelen.