Hoofdstuk 2: Correlatie: Correlatie
Richting van een lineaire verband
Om de richting van een lineair verband tussen twee numerieke variabelen te bepalen, berekenen we de covariantie.
Covariantie
Definitie
De covariantie stelts ons in staat om de richting van de lineaire relatie tussen twee kwantitatieve variabelen te bepalen.
De populatie covariantie en de steekproef covariantie tussen twee variabelen #X# en #Y# worden respectievelijk aangeduid met #\sigma_{\small{X,Y}}# en #s_{\small{X,Y}}#.
Formule
\[s_{\small{X,Y}}=\dfrac{\displaystyle\sum_{i=1}^n{(X_i-\bar{X})(Y_i-\bar{Y})}}{n-1}\]
Interpretatie van de covariantie
Het teken van de covariantie geeft de richting van het lineaire verband aan:
- Als #s_{\small{X,Y}}>0# dan hebben #X# en #Y# een positieve lineaire relatie.
- Als #s_{\small{X,Y}}<0# dan hebben #X# en #Y# een negatieve lineaire relatie.
- Als #s_{\small{X,Y}}=0# dan zijn #X# en #Y# lineair ongerelateerd.
De (absolute) waarde van de covariantie is echter geen goede maat voor de kracht van een lineair verband. Dit komt doordat de waarde van de covariantie sterk afhangt van de schaal waarop de variabelen gemeten zijn.
Het onderstaande voorbeeld illustreert waarom we de (absolute) waarde van de covariantie niet moeten interpreteren als een maat voor de kracht van een lineair verband.
Stel dat we een dataset hebben met daarin de waarden van twee numerieke variabelen #X# en #Y#, die beiden in meters gemeten zijn. Wanneer we de covariantie tussen deze twee variabelen berekenen, vinden een waarde van #s_{X,Y}=5#.
Vervolgens veranderen we echter van gedachten, en besluiten we de metingen van #X# en #Y# niet in meters maar in centimeters uit te drukken. Dit doen we door alle waarden voor #X# en #Y# met een factor #100# te vermenigvuldigen. Als we nu opnieuw de covariantie zouden berekenen, dan zouden we een waarde vinden van #s_{X,Y}=50000#.
Zoals je kan zien, is door elke waarde in de dataset met een factor #100# te vermenigvuldigen, de covariantie met een factor #100^2 = 10\,000# toegenomen. Dit betekent echter niet dat de kracht van de relatie tussen de variabelen met een factor #10\,000# is toegenomen. Sterker nog, de kracht van de relatie tussen de twee variabelen is exact hetzelfde als voor de transformatie van de data.
\[\text{}\]
Berekening van de steekproef covariantie
Om de steekproef covariantie tussen twee variabelen #X# en #Y# handmatig te berekenen, moeten we eerst voor elke waarneming van beide variabelen de afwijking van het gemiddelde bepalen.
Als de dataset totaal #n# paar waarnemingen bevat, dan berekenen we dus:
\[X_i - \bar{X} \,\,\,\,\,\,\,\,\text{en}\,\,\,\,\,\,\,\, Y_i - \bar{Y}\] voor #i = 1, \ldots, n#.
Vervolgens gaan we voor elk paar waarnemingen de afwijkingsscore van #X# vermenigvuldigen met de afwijkingsscore van #Y#:
\[(X_i - \bar{X})(Y_i - \bar{Y})\] voor #i = 1, \ldots, n#.
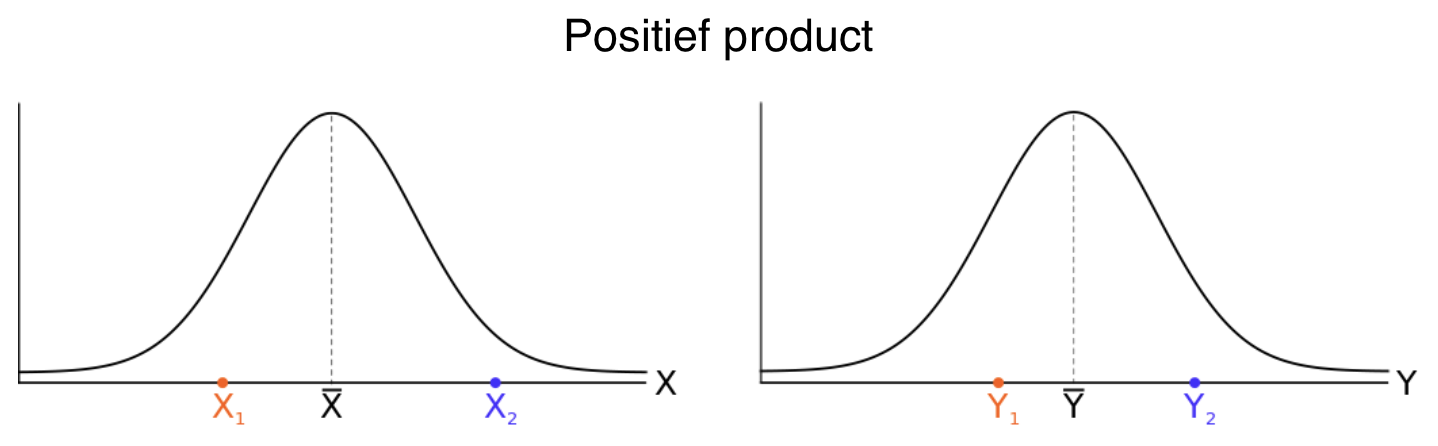
Als voor een bepaald paar waarnemingen beide scores aan dezelfde kant van hun respectievelijke gemiddelde liggen, dan wordt product van de afwijkingsscores positief:
- Als beide scores ( #\orange{X_1}#, #\orange{Y_1}# ) #\orange{\text{onder}}# hun respectieve gemiddelden liggen, dan zijn beide afwijkingsscores #\orange{\text{negatief}}#, en het product van de twee afwijkingen dus positief.
- Als beide scores ( #\purple{X_2}#, #\purple{Y_2}# ) #\purple{\text{boven}}# hun respectieve gemiddelden liggen, dan zijn beide afwijkingsscores #\purple{\text{positief}}#, en het product van de twee afwijkingen dus ook.
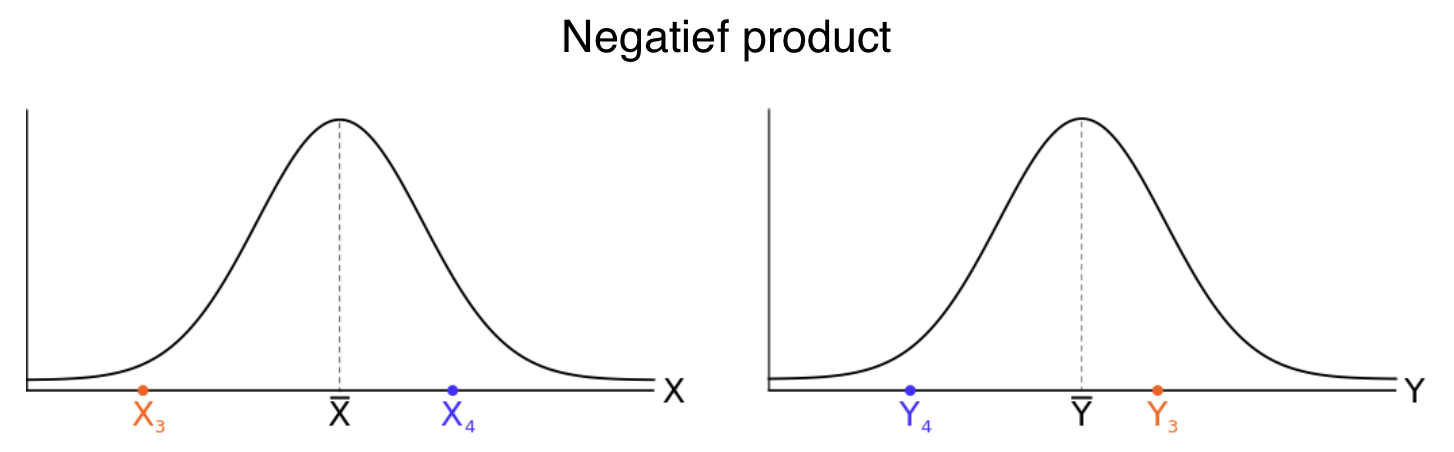
Wanneer de scores aan weerszijden van hun respectievelijke gemiddelde liggen, dan is één afwijkingsscore negatief (#\orange{X_3}#, #\purple{Y_4}# ) en de andere affwijkingsscore positief ( #\orange{Y_3}#, #\purple{X_4}# ), met als gevolg dat het product van de afwijkingen negatief zal zijn.
Tot slot berekenen we het gemiddelde van deze producten om de covariantie te bepalen:
\[s_{\small{X,Y}}=\dfrac{\displaystyle\sum_{i=1}^n{(X_i-\bar{X})(Y_i-\bar{Y})}}{n-1}\]
Om de steekproef covariantie tussen twee variabelen #X# en #Y# te berekenen in R, gebruiken we de volgende functie:
cov(x, y)
- x: De numerieke vector met de waardes voor variabele #X#
- y: De numerieke vector met de waardes voor variabele #Y#
Gegeven zijn de volgende #5# paar waarnemingen:
\[\begin{array}{|c|c|}
\hline
X&\,Y\,\\
\hline
7&5\\
3&9\\
6&6\\
2&1\\
2&4\\
\hline
\end{array}\]
Bereken de steekproef covariantie tussen #X# en #Y#.
Bereken eerst de gemiddelden van #X# en #Y#:
\[\begin{array}{rcl}
\bar{X}&=&\cfrac{\sum{X}}{n} = \dfrac{7+3+6+2+2}{5}=\dfrac{20}{5}=4\\\\
\bar{Y}&=&\cfrac{\sum{Y}}{n} = \dfrac{5+9+6+1+4}{5}=\dfrac{25}{5}=5
\end{array}\]
Nu dat de gemiddelde bekend zijn, kunnen we waarde van #(X-\bar{X}), (Y-\bar{Y})#, and #(X-\bar{X})(Y-\bar{Y})# berekenen:
\[\begin{array}{|c|c|c|c|c|}
\hline
X&Y&X-\bar{X}&Y-\bar{Y}&(X-\bar{X})(Y-\bar{Y})\\
\hline
7&5&3&0&0\\
3&9&-1&4&-4\\
6&6&2&1&2\\
2&1&-2&-4&8\\
2&4&-2&-1&2\\
\hline
\end{array}\]
Bereken tot slot de steekproef covariantie:
\[\begin{array}{rcl}
s_{X,Y}&=&\dfrac{\sum\limits_{i=1}^n{(X_i-\bar{X})(Y_i-\bar{Y})}}{n-1}\\
\\
&=&\dfrac{0-4+2+8+2}{5-1}\\
\\
&=&\dfrac{8}{4}\\
\\
&=&2.00\\
\end{array}\]
omptest.org als je een OMPT examen moet maken.
