Hoofdstuk 3: Kansrekening: Willekeurigheid
Verzamelingen, deelverzamelingen en elementen
Voordat we het gebrip willekeurigheid introduceren, is het belangrijk om eerst de termen verzameling, element, en deelverzameling te definiëren.
Verzameling en Elementen
Definitie
Een verzameling is een collectie afzonderlijke objecten. Een object kan alles zijn, waaronder een getal, een letter, een verzameling, of een combinatie hiervan.
De afzonderlijke objecten in een verzameling worden de elementen van die verzameling genoemd.
Notatie
\[\text{verzameling}=\{\text{element}, \text{element}, \ldots\}\]
Bijvoorbeeld, de getallen #2#, #4# en #6# zijn afzonderlijke objecten. Als we deze objecten samennemen, dan voemen zij een verzameling met drie elementen, geschreven als #\{2,4,6\}#.
\[\text{}\]
Venn diagram
Verzamelingen van elementen worden vaak afgebeeld met behulp van een Venn diagram.
Verzamelingen krijgen gewoonlijk een naam (bijv #A#) en worden weergegeven als een cirkel. De elementen van de verzameling (bijv #1, 2, 3, 4, 5, 6#) worden vervolgens in de cirkel geplaatsts.
Het Venn diagram hieronder correspondeert met de verzameling #A = \{1, 2, 3, 4, 5, 6\}#.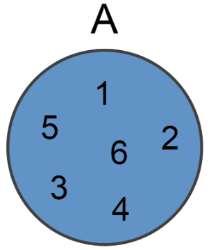
De verzameling #B# is een deelverzameling van #A# als #B# volledig binnen #A# valt. Dat wil zeggen, als alle elementen van #B# ook elementen van #A# zijn.
Deelverzamelingen worden in een Venn diagram gerepresenteerd als een cirkel in een cirkel.
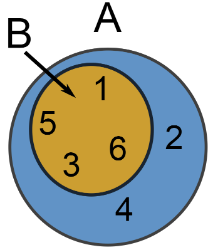
De afbeelding hieronder toont de verzameling #A = \{1, 2, 3, 4, 5, 6\}# en de deelverzameling#B = \{1, 3, 5, 6\}#.
omptest.org als je een OMPT examen moet maken.
