Hoofdstuk 3: Kansrekening: Relaties tussen gebeurtenissen
Complement van een gebeurtenis
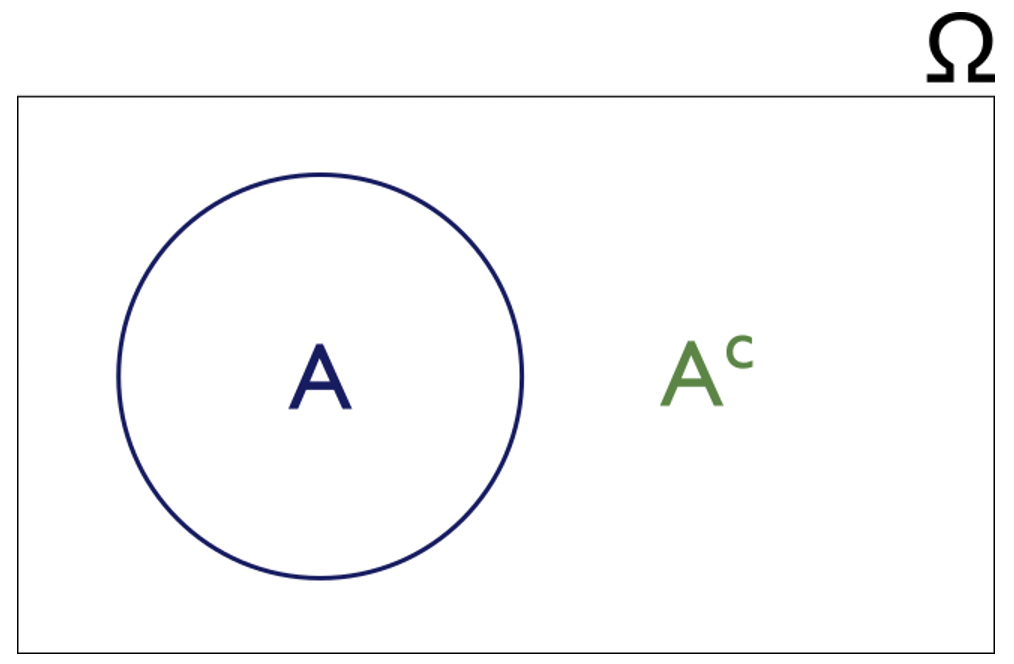
Laat #A# een gebeurtenis zijn, dan is de verzameling van alle mogelijke uitkomsten waarbij #A# niet gebeurt, het complement van #A#.
Complement van een gebeurtenis
Definitie
Het complement van een gebeurtenis #A# is de verzameling van alle uitkomsten in de uitkomstenruimte #\Omega# die geen onderdeel uitmaken van #A#.
Notatie
#A^c#
De uitkomstenruimte van dit experiment is:
\[\Omega =\{\text{K, M}\}\]
De uitkomst behorende bij gebeurtenis #A# is:
\[A=\text{'Kop komt boven'}=\{\text{K}\}\]
Het complement van #A# is de verzameling van alle uitkomsten in #\Omega# die geen deel uitmaken van #A#:
\[A^c = \text{'Kop komt NIET boven'} = \text{'Munt komt boven'} = \{\text{M}\}\]
Ontgrendel volledige toegang
Toegang voor leraar
Vraag een demo account aan. Wij helpen je graag op weg met onze digitale leeromgeving.
Toegang voor student
Is jouw universiteit niet aangesloten?
Via Pass Your Math kan je toegang krijgen tot onze cursussen onafhankelijk van je onderwijsinstelling. Bekijk de prijzen en nog veel meer. Of ga naar
omptest.org als je een OMPT examen moet maken.
omptest.org als je een OMPT examen moet maken.
