Hoofdstuk 5: Steekproeven: Steekproefverdelingen
Steekproefverdeling van het Steekproefgemiddelde
Bij gebruik van een steekproefgemiddelde om een populatie gemiddelde te schatten, kan de steekproefverdeling van het steekproefgemiddelde worden gebruikt om te bepalen hoeveel inschattingsfout redelijkerwijs te verwachten is.
#\phantom{0}#
Steekproefverdeling van het Steekproefgemiddelde
De steekproefverdeling van het steekproefgemiddelde is de kansverdeling van het steekproefgemiddelde van alle mogelijke steekproeven van een bepaalde grootte #n# die uit een populatie kunnen worden getrokken.
Het gemiddelde van de verdeling van steekproefgemiddelden wordt de verwachte waarde van het steekproefgemiddelde genoemd en wordt aangeduid als #\mu_{\bar{X}}#.
De standaardafwijking van de verdeling van steekproefgemiddelden wordt de standaardfout van het gemiddelde genoemd en wordt aangeduid als #\sigma_{\bar{X}}#. De standaardfout is een maat voor hoeveel verschil te verwachten valt tussen een steekproefgemiddelde #\bar{X}# en het bevolkingsgemiddelde #\mu#.
Normaal Verdeelde Populatie
Wanneer een steekproef van grootte #n# wordt getrokken uit een populatie die normaal verdeeld is met parameters #\mu# en #\sigma#, dan heeft vervolgens de steekproefverdeling van #\bar{X}# de volgende kenmerken:
- Vorm. De steekproefverdeling van het steekproefgemiddelde is normaal verdeeld.
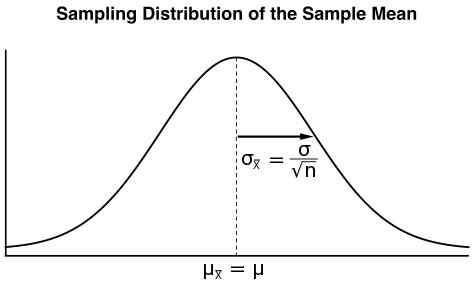
- Centrale tendens. Het gemiddelde van de steekproefverdeling, #\mu_{\bar{X}}#, is gelijk aan het populatiegemiddelde #\mu#.
\[\mu_{\bar{X}} = \mu\] - Variabiliteit. De standaardafwijking van de steekproefverdeling, #\sigma_{\bar{X}}#, wordt als volgt berekend:
\[\sigma_{\bar{X}} = \cfrac{\sigma}{\sqrt{n}}\]
\[\bar{X} \sim N(\mu, \cfrac{\sigma}{\sqrt{n}})\]
Bepaal de verwachte waarde van het steekproefgemiddelde, #\mu_{\bar{X}}#, en de standaardfout van het steekproefgemiddelde, #\sigma_{\bar{X}}#.
#\mu_{\bar{X}} = 50#
#\sigma_{\bar{X}} = 2.5820#
Aangezien de populatie waaruit de steekproef getrokken is normaal verdeeld is, weten we dat de steekproefverdeling van het steekproefgemiddelde ook normaal verdeeld is.
De verwachte waarde van het steekproefgemiddelde, #\mu_{\bar{X}}#, is gelijk aan het populatiegemiddelde #\mu#:
\[\mu_{\bar{X}} = \mu = 50\]
De standaardfout van het steekproefgemiddelde, #\sigma_{\bar{X}}#, wordt als volgt berekend:
\[\sigma_{\bar{X}}=\dfrac{\sigma}{\sqrt{n}}=\dfrac{20}{\sqrt{60}}=2.5820\]
Dus #\bar{X} \sim N(50, 2.5820)#.
#\phantom{0}#
Stel dat, echter, een steekproef wordt getrokken uit een populatie die niet normaal verdeeld is. In deze gevallen kan de centrale limietstelling worden toegepast om de kenmerken van de steekproefverdeling van het steekproefgemiddelde te bepalen.
#\phantom{0}#
Centrale Limietstelling
De centrale limietstelling zegt dat, als de steekproefgrootte toeneemt, de steekproefverdeling van het steekproefgemiddelde een normale verdeling benadert met een gemiddelde van #\mu_{\bar{X}}=\mu# en een standaardafwijking van #\sigma_{\bar{X}}=\sigma/\sqrt{n}#, ongeacht de vorm van de populatie waaruit de steekproef is getrokken.
Een steekproefgrootte van #30# of meer is groot genoeg om de steekproefverdeling van het steekproefgemiddede bij benadering als normaal te beschouwen.
Bepaal de verwachte waarde van het steekproefgemiddelde, #\mu_{\bar{X}}#, en de standaardfout van het steekproefgemiddelde, #\sigma_{\bar{X}}#.
#\mu_{\bar{X}} = 140#
#\sigma_{\bar{X}} = 0.6455#
Een steekproefgrootte van #n=60# wordt als groot genoeg beschouwd om de centrale limietstelling toe te passen.
Dit betekent dat, hoewel de steekproef in kwestie afkomstig is uit een populatie met een rechtsscheve verdeling is de steekproefverdeling van het steekproefgemiddelde ongeveer normaal.
Nu we weten dat de steekproefverdeling van het steekproefgemiddelde ongeveer normaal is, kunnen we de eigenschappen ervan bepalen:
- #\mu_{\bar{X}} = \mu = 140#
- #\sigma_{\bar{X}} = \cfrac{\sigma}{\sqrt{n}} = \cfrac{5}{\sqrt{60}} = 0.6455#
Dus #\bar{X} \sim N(140, 0.6455)#.
omptest.org als je een OMPT examen moet maken.
