Hoofdstuk 6: Schatten en betrouwbaarheidsintervallen: Schatten
Het Maken van een 95% Betrouwbaarheidsinterval voor het Populatiegemiddelde
Om een #95\%# betrouwbaarheidsinterval te maken voor het populatiegemiddelde #\mu# zullen we gebruik moeten maken van de steekproef verdeling van het steekproefgemiddelde.
Voor het doel van dit voorbeeld, nemen we aan dat de voorwaarden voor normaliteit zijn voldaan en het steekproefgemiddelde #\bar{X}# (ongeveer) de #N(\mu,\sigma/\sqrt{n})# distributie heeft.
#\phantom{0}#
De bouw van een 95% betrouwbaarheidsinterval voor het populatiegemiddelde
Laat #Z# de gestandaardiseerde versie van #\bar{X}# zijn, dat wil zeggen:
\[Z = \cfrac{\bar{X} - \mu}{\sigma_{\bar{X}}} =\cfrac{\bar{X} - \mu}{\sigma/\sqrt{n}}\]
Dan heeft #Z# de standaard normale distributie, dat is #Z\sim N(0,1)#.
Aangetoond kan worden#^{1}# dat de middelste #95\%# van de standaard normale verdeling tussen #-1.96# en #1.96# ligt:
\[\mathbb{P}(-1.96 \leq Z \leq 1.96) = 0.95\]
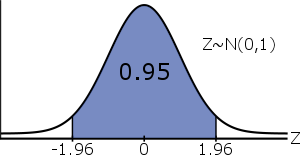
Vervangen van #Z# met #\cfrac{\bar{X} - \mu}{\sigma/\sqrt{n}}# geeft:
\[\mathbb{P}(-1.96 \leq \cfrac{\bar{X} - \mu}{\sigma/\sqrt{n}} \leq 1.96) = 0.95\]
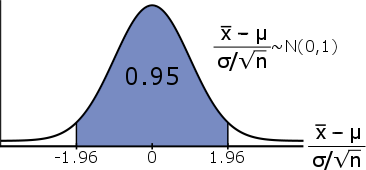
Met de hulp van een beetje algebra#^{2}#, kan dit worden herschreven als:
\[\mathbb{P}(\mu -1.96\cdot\cfrac{\sigma}{\sqrt{n}} \leq \bar{X} \leq \mu + 1.96\cdot\cfrac{\sigma}{\sqrt{n}}) = 0.95\]
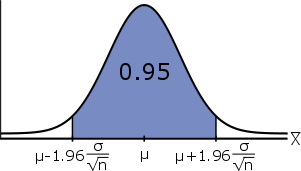
Dit resultaat is wiskundig gelijk aan:
\[\mathbb{P}(\bar{X} -1.96\cdot\cfrac{\sigma}{\sqrt{n}} \leq \mu \leq \bar{X} + 1.96\cdot\cfrac{\sigma}{\sqrt{n}}) = 0.95\]
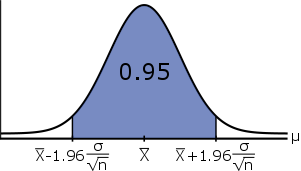
In woorden, is er #95\%# kans dat we een aselecte steekproef nemen, zodat het interval
\[CI_{\mu,95\%}=(L,U)=(\bar{X} -1.96\cdot\cfrac{\sigma}{\sqrt{n}},\,\,\,\, \bar{X} + 1.96\cdot\cfrac{\sigma}{\sqrt{n}})\]
de werkelijke waarde van het populatiegemiddelde #\mu# bevat .
Nadat het monster is genomen en de waarden van de ondergrens #L# en de bovengrens #U# zijn berekend, wordt het interval #(L,U)# een #95\%# betrouwbaarheidsinterval genoemd voor #\mu#.
De uitdrukking #1.96 \cdot \cfrac{\sigma}{\sqrt{n}}# wordt de foutmarge genoemd, terwijl #95\%# het betrouwbaarheidsniveau wordt genoemd.
omptest.org als je een OMPT examen moet maken.
