Hoofdstuk 7: Hypothese toetsen: Introductie in Hypothese toetsen (p-waarde benadering)
Instellen van de Criteria voor een Besluit
Zodra de hypotheses van de test zijn geformuleerd, is de volgende stap om de criteria in te stellen voor een beslissing. Dit moet altijd worden gedaan voordat de steekproefgegevens worden verzameld.
In het bijzonder, moeten we bepalen welke waarden van de steekproefparameter leiden tot de verwerping van de nulhypothese. Omdat een steekproef een onvolledig beeld geeft van een populatie, is enig verschil tussen een steekproefparameter en de bijbehorende bevolkingsparameter te verwachten.
Hoeveel verschil redelijkerwijs verwacht kan worden wordt afgeleid uit de steekproefverdeling van de steekproefparameter onder de nulhypothese. Indien de nulhypothese juist is, is het waarschijnlijk dat de steekproefwaarde relatief dicht overeenkomt met de gemiddelde waarde van de steekproefverdeling.
Als het verschil tussen een steekproefparameter en het gemiddelde van de veronderstelde steekproefverdeling toeneemt, moet het vertrouwen in de nulhypothese afnemen. Als je een steekproefstatistiek waarneemt die uiterst onwaarschijnlijk is gezien het feit dat de nulhypothese juist is, moet dit leiden tot de afwijzing van de nulhypothese. 
Om te formaliseren wat een uiterst onwaarschijnlijk resultaat inhoudt, moet het significantieniveau van de test worden ingesteld.
#\phantom{0}#
Significantieniveau
Het significantieniveau, aangeduid met #\alpha#, van een statistische test is de kansdrempel die bepaalt hoe onwaarschijnlijk een steekproefparameter moet zijn om de nulhypothese #H_0# af te wijzen.
Het bereik van waarden voor de steekproefwaarde dat zal leiden tot afwijzing van de nulhypothese wordt het kritiek gebied genoemd. De grenswaarden van het kritiek gebied worden grenswaarden genoemd.
Het verlagen van het significantieniveau verkleint het kritiek gebied van de steekproefverdeling, waardoor een kleiner bereik van waarden leidt tot afwijzing van #H_0#.
Het verhogen van het significantieniveau vergroot het kritiek gebied van de steekproefverdeling, waardoor een groter bereik van waarden leidt tot afwijzing van #H_0#.
Het instellen van een #\alpha = 0.05# significantieniveau betekent dat als je een steekproefparameter waarneemt die een #5\%# kans of minder heeft van het waar zijn van de nulhypothese, de nulhypothese moet worden verworpen.
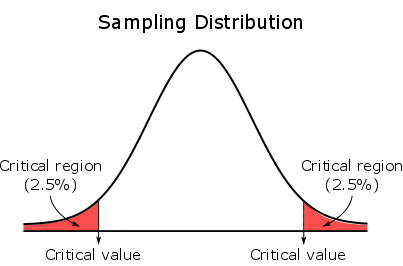
Voor een tweezijdige toets, wordt het kritische gebied gelijk verdeeld tussen de twee staarten.
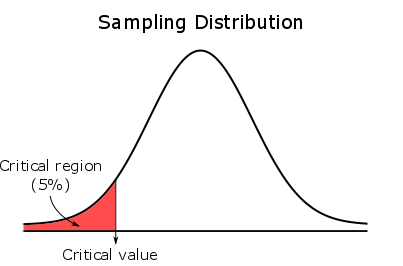
Voor een linkszijdige toets, is het gehele kritische gebied in de linkerstaart.
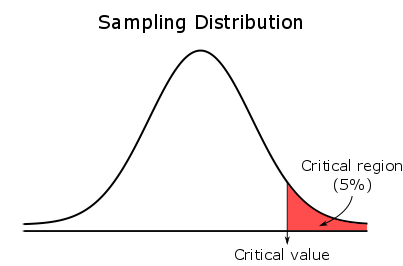
Voor een rechtszijdige toets, is het gehele kritische gebied in de rechter staart.
Kiezen van een Geschikt Significantieniveau
Merk dat de keuze van het significantieniveau #\alpha# moet worden gemaakt met zorg. Hoe sterker de alternatieve hypothese, hoe kleiner #\alpha# zou moeten zijn.
Bijvoorbeeld #H_a: \mu \gt \mu_0# is een sterkere hypothese dan #H_a: \mu \neq \mu_0#, omdat de eerste hypothese niet alleen bepaalt dat #\mu# verschilt van #\mu_0# maar dat #\mu# verschilt van #\mu_0# in een bepaalde richting. Dus een kleinere #\alpha# moet worden gebruikt voor een eenzijdige toets dan wat moet worden gebruikt voor een tweezijdige toets.
Een bijkomende overweging is de ernst van de gevolgen als een conclusie wordt gemaakt ten gunste van #H_a#, maar deze beslissing een vergissing blijkt te zijn. Als ernstige schade zou kunnen worden veroorzaakt (zoals schade aan iemands gezondheid, verlies van grote sommen geld), dan moet een kleinere #\alpha# worden gebruikt.
Aan de andere kant, gebruik van een te kleine #\alpha# zou ook ernstige gevolgen kunnen hebben, omdat het besluiten in het voordeel van #H_0# wanneer #H_a# eigenlijk waar is, bijvoorbeeld kan leiden tot het falen van een behandeling voor een ziekte die effectief geweest zou zijn.
omptest.org als je een OMPT examen moet maken.
