Hoofdstuk 7: Hypothese toetsen: Introductie in Hypothese toetsen (p-waarde benadering)
Het berekenen van de p-waarde en het Maken van een Besluit
p-waarde
De #\boldsymbol{p}#-waarde van een toets is de waarschijnlijkheid, wanneer de nulhypothese #H_0# wordt aangenomen waar te zijn, van het observeren van een toestingsgrootheid gelijk aan of meer extreem dan werkelijk waargenomen.
Voor een tweezijdige toets, is de #p#-waarde een twee-zijdige kans, wat betekent dat het gelijk verdeeld wordt tussen de twee staarten.
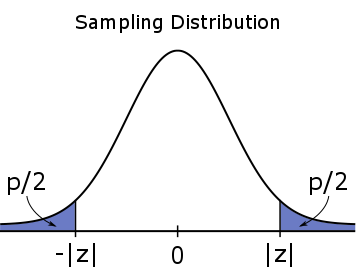
#H_a: \mu \neq \mu_0#
Voor een eenzijdige toets, is de #p#-waarde een eenzijdige kans, wat betekent dat het geheel is gelegen in een van de staarten.
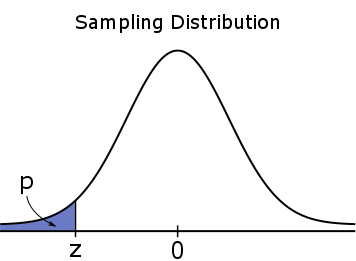
#H_a: \mu \lt \mu_0#
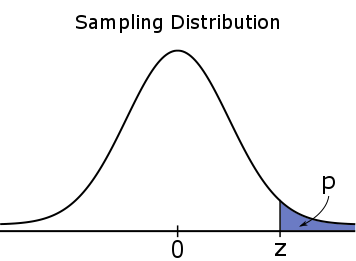
#H_a: \mu \gt \mu_0#
Interpretatie van een p-waarde
De #p# -waarde is niet de kans dat de nulhypothese #H_0# onwaar is. De waarheid van #H_0# is niet willekeurig.
De steekproef is willekeurig, dus als gevolg is de toetsingsgrootheid willekeurig. Dus de #p#-waarde heeft betrekking op de toetsingsgrootheid.
Een kleine #p#-waarde betekent dat de waarde van de toestsingsgrootheid niet in het bereik ligt van waarden die we zouden verwachten als #H_0# waar is.
Het Berekenen van de p-waarde van een Z-toets voor een Populatiegemiddelde met Statistische Software
De berekening van de #p#-waarde van een #Z#-toets voor #\mu# is afhankelijk van de richting van de toetsen en kunnen worden uitgevoerd met behulp van Excel of R.
Voor de berekening van de #p#-waarde van een #Z#-toets voor #\mu# in Excel, gebruik je een van de volgende functies:
\[\begin{array}{lllll}
\phantom{0}\text{Richting}&\phantom{0000}H_0&\phantom{0000}H_a&\phantom{000}p\text{-value}&\phantom{0000000000}\text{Excel Functie}\\
\hline
\text{Twee-zijdig}&H_0:\mu = \mu_0&H_a:\mu \neq \mu_0&2\cdot \mathbb{P}(Z\geq |z|)&=2 \text{ * }(1 \text{ - }\text{NORM.DIST}(\text{ABS}(z),0,1,1))\\
\text{Links-zijdig}&H_0:\mu \geq \mu_0&H_a:\mu \lt \mu_0&\mathbb{P}(Z\leq z)&=\text{NORM.DIST}(z,0,1,1)\\
\text{Rechts-zijdig}&H_0:\mu \leq \mu_0&H_a:\mu \gt \mu_0&\mathbb{P}(Z\geq z)&=1 \text{ - }\text{NORM.DIST}(z,0,1,1)\\
\end{array}\]
Voor de berekening van een #p#-waarde van een #Z#-toets voor #\mu# in R, gebruik je een van de volgende functies:
# \begin{array}{lllll}
\phantom{0}\text{Richting}&\phantom{0000}H_0&\phantom{0000}H_a&\phantom{000}p\text{-value}&\phantom{0000000}\text{R Functie}\\
\hline
\text{Twee-zijdig}&H_0:\mu = \mu_0&H_a:\mu \neq \mu_0&2\cdot \mathbb{P}(Z\geq |z|)&2 \text{ * }\text{pnorm}(\text{abs}(z),0,1, \text{FALSE})\\
\text{Links-zijdig}&H_0:\mu \geq \mu_0&H_a:\mu \lt \mu_0&\mathbb{P}(Z\leq z)&\text{pnorm}(z,0,1, \text{TRUE})\\
\text{Rechts-zijdig}&H_0:\mu \leq \mu_0&H_a:\mu \gt \mu_0&\mathbb{P}(Z\geq z)&\text{pnorm}(z,0,1, \text{FALSE})\\
\end{array} #
Opmerking: #|z|# is de absolute waarde van #z#, namelijk de afstand van #z# tot #0#, ongeacht of #z < 0# of #z > 0#.
#\phantom{0}#
Zodra de #p#-waarde van de test is berekend, is het tijd om een beslissing te maken over de nulhypothese #H_0#.
#\phantom{0}#
Een Beslissing Maken
Als de berekende #p#-waarde kleiner of gelijk is aan het significantieniveau (dwz #p \leq \alpha# ), betekent dit dat de waargenomen gegevens zeer onwaarschijnlijk zijn, indien #H_0# waar is. We zeggen dan dat we #H_0# verwerpen ten gunste van #H_a#.
Als de berekende #p# -waarde groter is dan het significantieniveau (dwz #p \gt \alpha# ), betekent dit dat de waargenomen gegevens in het bereik van waarden vallen die wij verwachten waar te nemen indien #H_0# waar is. Vervolgens zeggen we dus dat we #H_0# niet verwerpen.
Een onderzoeker verzamelt watermonsters van één liter op willekeurig geselecteerde #195# locaties langs een rivier en meet de hoeveelheid opgeloste zuurstof in elk monster.
De onderzoeker is van plan een #Z#-test te gebruiken om te bepalen of het gemiddelde zuurstofgehalte van de rivier significant verschilt van #7# mg per liter, op het #\alpha = 0.04# significantieniveau.
Het steekproefgemiddelde #\bar{X}# blijkt #7.10# mg per liter te zijn.
Bereken de #p#-waarde van de test en neem een beslissing over #H_0#. Rond je antwoord af op #4# decimalen.
Op basis van deze #p#-waarde, moet #H_0# wel worden verworpen, omdat #\,p# #\lt# #\alpha#.
Er zijn een aantal verschillende manieren waarop we de #p#-waarde van de test kunnen berekenen. Klik op een van de panelen om naar een specifieke oplossing te gaan.
Omdat de steekproef getrokken is uit een normaal verdeelde populatie, weten we dat de teststatistiek
\[Z=\cfrac{\bar{X} - \mu_0}{\sigma/\sqrt{n}}\]
de #N(0,1)# verdeling heeft, onder de aanname dat #H_0# waar is.
Bereken de waarde van teststatistiek #z#:
\[z = \cfrac{\bar{X}-\mu_0}{\sigma/\sqrt{n}} =\cfrac{7.10 - 7}{0.61/\sqrt{195}} = 2.28922\]
Voor een tweezijdige #Z#-test, wordt de #p#-waarde gedefinieerd als #2\cdot \mathbb{P}(Z \geq |z|)#. Om deze waarde in Excel te berekenen, gebruik je de volgende functie:
NORM.DIST(x, mean, standard_dev, cumulative)
- x: De waarde waarin je de verdelingsfunctie wilt evalueren.
- mean: Het gemiddelde van de verdeling.
- standard_dev: De standaardafwijking van de verdeling.
- cumulative: Een logische waarde die de vorm van de functie bepaalt.
- WAAR - gebruikt de cumulatieve verdelingsfunctie, #\mathbb{P}(X \leq x)#
- ONWAAR - gebruikt de kansdichtheidsfunctie
Dus om #p = 2\cdot \mathbb{P}(Z \geq |z|)# te berekenen, voer je het volgende command uit:
\[
=2 \text{ * }(1 \text{ - } \text{NORM.DIST}(\text{ABS}(z),0,1,1))\\
\downarrow\\
=2 \text{ * }(1 \text{ - } \text{NORM.DIST}(\text{ABS}(2.28922),0,1,1))
\]
Dit geeft:
\[p = 0.0221\]
Aangezien #\,p# #\lt# #\alpha#, moet #H_0: \mu = 7# wel worden verworpen.
Omdat de steekproef getrokken is uit een normaal verdeelde populatie, weten we dat de teststatistiek
\[Z=\cfrac{\bar{X} - \mu_0}{\sigma/\sqrt{n}}\]
de #N(0,1)# verdeling heeft, onder de aanname dat #H_0# waar is.
Bereken de waarde van teststatistiek #z#:
\[z = \cfrac{\bar{X}-\mu_0}{\sigma/\sqrt{n}} =\cfrac{7.10 - 7}{0.61/\sqrt{195}} = 2.28922\]
Voor een tweezijdige #Z#-test, wordt de #p#-waarde gedefinieerd als #2\cdot \mathbb{P}(Z \geq |z|)#. Gebruik de volgende functie om deze waarde in R te berekenen:
pnorm(q, mean, sd, lower.tail)
- q: De waarde waarin je de verdelingsfunctie wilt evalueren.
- mean: Het gemiddelde van de verdeling.
- sd: De standaardafwijking van de verdeling.
- lower.tail: Indien WAAR (standaard) geldt, zijn de kansen #\mathbb{P}(X \leq x)#, anders #\mathbb{P}(X \gt x)#.
Dus om #p = 2\cdot \mathbb{P}(Z \geq |z|)# te berekenen, voer je het volgende command uit:
\[
2 \text{ * } \text{pnorm}(q = \text{abs}(z), mean = 0, sd = 1,lower.tail = \text{ONWAAR})\\
\downarrow\\
2\text{ * } \text{pnorm}(q = \text{abs}(2.28922), mean = 0, sd = 1,lower.tail = \text{ONWAAR})
\]
Dit geeft:
\[p = 0.0221\]
Aangezien #\,p# #\lt# #\alpha#, moet #H_0: \mu = 7# wel worden verworpen.
omptest.org als je een OMPT examen moet maken.
