Hoofdstuk 7: Hypothese toetsen: Introductie in Hypothese Toetsen (Kritiek Gebied benadering)
 Het Bepalen van het Kritiek Gebied
Het Bepalen van het Kritiek Gebied
Zodra de hypotheses zijn geformuleerd, is de volgende stap het bepalen van de criteria voor een besluit. In het bijzonder, moet je bepalen welke waarden van de steekproefparameter zullen leiden tot de verwerping van de nulhypothese. Omdat een steekproef een onvolledig beeld geeft van een populatie, is enig verschil tussen een steekproefparameter en de bijbehorende bevolkingsparameter te verwachten.
Hoeveel verschil redelijkerwijs te verwachten is als de nulhypothese waar is kan worden afgeleid uit de steekproefverdeling van de steekproefparameter. Indien de nulhypothese juist is, is het waarschijnlijk dat de steekproefwaarde relatief dicht overeenkomt met het gemiddelde van de steekproefverdeling.
Als het verschil tussen een steekproefparameter en het gemiddelde van de veronderstelde steekproefverdeling toeneemt zal de waarschijnlijkheid dat de nulhypothese waar is afnemen. Indien een steekproef een parameter produceert die uiterst onwaarschijnlijk is gezien het feit dat de nulhypothese waar is, moet dit leiden tot de afwijzing van de nulhypothese.
Om te formaliseren wat een uiterst onwaarschijnlijk resultaat is, moet het significantieniveau van de toets worden ingesteld.
#\phantom{0}#
Alpha-niveau
Definitie
Het significantieniveau of alfa niveau van een statistische toets is de kansdrempel die bepaalt hoe onwaarschijnlijk een steekproefparameter moet zijn om de nulhypothese te verwerpen.
Notatie
#\alpha#
#\phantom{0}#
Bijvoorbeeld, het instellen van een alfa-niveau van #\alpha = 0.05# betekent dat als je een steekproefparameter vindt die een #5\%# of minder kans heeft van optreden, indien de nulhypothese juist is, moet de nulhypothese worden verworpen.
Het verlagen van het alfa-niveau betekent dat sterker bewijs is vereist om de nulhypothese te verwerpen. Zodra het alfa-niveau van de test is ingesteld, is de volgende stap het bepalen van het kritiek gebied van de steekproefverdeling.
#\phantom{0}#
Kritiek gebied
Definitie
Het kritiek gebied van een steekproefverdeling bevat de waarden voor de steekproefwaarde die zo onwaarschijnlijk zijn indien de nulhypothese juist is, dat het vinden van een van deze waarden zal leiden tot afwijzing van de nulhypothese.
De grenzen van het kritische gebied worden grenswaarden genoemd.
Grafische weergave
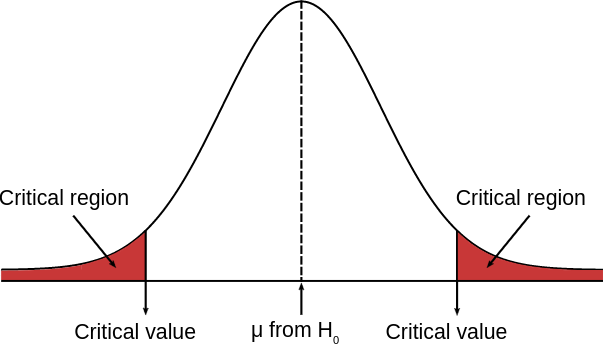
#\phantom{0}#
Bij het uitvoeren van een #z#-toets, wordt de Standaardnormale tabel gebruikt om de grenzen van het kritiek gebied te bepalen. Voor een #z#-toets, wordt de locatie van de grenzen volledig bepaald door de alfaniveau van de test. De tabel hieronder toont de meest gebruikte significantieniveaus en de bijbehorende grenswaarden.
\[\begin{array}{c|c}
\alpha&\text{Critical }z \text{ values}\\
\hline
0.10&\pm 1.645\\
0.05&\pm 1.96\\
0.01&\pm 2.58\\
\end{array}\]
3. Kritiek Gebied
Als de nulhypothese waar is, moet de Zomer Cursus geen effect hebben op de cijfers van de studenten en de bevolking van de studenten die deelnemen aan de Zomer Cursus zal identiek zijn aan die van de oorspronkelijke bevolking van studenten; dat is, een normale verdeling met #\mu = 6.5# en #\sigma=1#.
Vervolgens is het nodig om alle mogelijke uitkomsten te overwegen voor een steekproef van #n =100# studenten. Dit is de verdeling van de steekproef gemiddelden voor #n=100#. Indien de nulhypothese juist is, dan heeft de verdeling van steekproefgemiddelden de volgende eigenschappen:
#\phantom{0}#
- #\mu_{\bar{X}}= \mu_0 = 6.5#
- #\sigma_{\bar{X}} = \cfrac{\sigma}{\sqrt{n}}=\cfrac{1}{\sqrt{100}} = 0.1#
Tenslotte wordt de verdeling van het steekproefgemiddelde gebruikt om het kritiek gebied van de proef te bepalen. De universiteit besluit het alfaniveau van de test in te stellen op #\alpha = 0.05#, waardoor het kritiek gebied bestaat uit de extreme #5\%# van de steekproefverdeling.
De grenswaarden voor een #Z#-toets met #\alpha =0.05# zijn #Z = \pm 1.96#. Dit betekent dat het vinden van een #Z#-score van minder dan #-1.96# of groter dan #1.96# zou leiden tot verwerping van de nulhypothese.

omptest.org als je een OMPT examen moet maken.





