Fouten in Besluitvorming

Hoofdstuk 7: Hypothese toetsen: Introductie in Hypothese Toetsen (Kritiek Gebied benadering)

Fouten in Besluitvorming

Inferentiële statistiek maakt gebruik van de beperkte informatie die een steekproef verstrekt om conclusies te trekken over een grotere populatie.

We verwachten niet dat steekproeven een perfecte representatie zijn van de populatie, echter, in sommige extreme gevallen zal de steekproef zeer verschillen van de populatie waaruit het genomen is. Zulke extreme steekproeven kunnen leiden tot onjuiste conclusies over de populatie.

Onthoud dat er twee mogelijke besluiten die kunnen worden gemaakt op basis van een hypothese toets:

De nulhypothese wordt verworpen.
De nulhypothese wordt niet verworpen.

Beide beslissingen kunndn ofwel goed of fout zijn, wat leidt tot vier mogelijke uitkomsten.

\[
\begin{array}{l|c|c}
&H_0\text{ is niet verworpen}&H_0\text{ is verworpen}\\
\hline
H_0 \text{ is waar}&\green{\text{Correct besluit}}&\red{\text{Type I error}}\\
H_0 \text{ is onwaar}&\red{\text{Type II error}}&\green{\text{Correct besluit}}\\
\end{array}
\]

Type I Fout

Een type I fout verwerpt de nulhypothese, terwijl het in feite is waar. Dit wordt ook wel een vals positief resultaat genoemd. De kans op het plegen van een Type I fout gelijk is aan het significantieniveau van de toets en wordt aangeduid met #\alpha#.

\[\alpha = \mathbb{P}(\text{Type I error})=\mathbb{P}(\text{reject }H_0\,|\,H_0\text{ is true})\]

Een type I fout is analoog aan een onschuldig persoon die schuldig wordt gevonden.

#\phantom{0}#

Type II Fout

Een type II fout verwerpt de nulhypothese niet, terwijl het in feite onjuist is. Dit wordt ook wel een vals negatief resultaat genoemd. De kans op het plegen van een Type II fout wordt aangeduid met #\beta#.

\[\beta = \mathbb{P}(\text{Type II error})=\mathbb{P}(\text{verwerp niet }H_0\,|\,H_0\text{ is onjuist})\]

Een Type II fout is analoog aan een schuldige die niet schuldig wordt bevonden.

#\phantom{0}#
Het verschil tussen de twee types fouten wordt geïllustreerd door het volgende boomdiagram: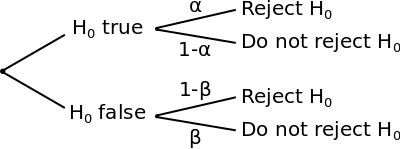

Het is misschien verleidelijk om de kans op een Type I fout te verminderen door een heel laag significantieniveau te kiezen.

Er is een compromis, echter, want het verminderen van de kans op een Type I fout verhoogt tegelijkertijd de kans op een Type II fout, en andersom.