Hoofdstuk 7: Hypothese toetsen: Hypothese Toets voor een Populatie Proportie
Grote Steekproef Proportie Toets: Toetsingsgrootheid en p-waarde
Stel je voor dat we een willekeurige steekproef nemen van grootte #n# uit een populatie waarvan een deel #\pi# een bepaald kenmerk vertoont.
Laat #X# duiden op het aantal successen uit #n# observaties, en laat #\hat{p}=\frac{X}{n}# duiden op de steekproef proportie.
Wanneer de steekproefgrootte groot is ( #n\geq 30# ), kan de centrale limietstelling worden toegepast, en kan een #Z#-toets worden gebruikt om bepaalde hypotheses te toetsen over de populatieproportie #\pi#.
#\phantom{0}#
Z-toets voor een Populatie Proportie: Toetsingsgrootheid
De toestingsgrootheid van een #Z#-toets voor een populatieproportie #\pi# wordt als volgt berekend:
\[Z=\cfrac{\hat{p}-\pi_0}{\sigma_{\hat{p}}}=\cfrac{\hat{p}-\pi_0}{\sqrt{\pi_0 \cdot (1 - \pi_0)/n}}\]
Onder de aanname dat de nulhypothese #H_0# waar is, heeft de steekproefverdeling van #Z# de Standaard Normaalverdeling. Dat wil zeggen, #Z \sim N(0,1)#.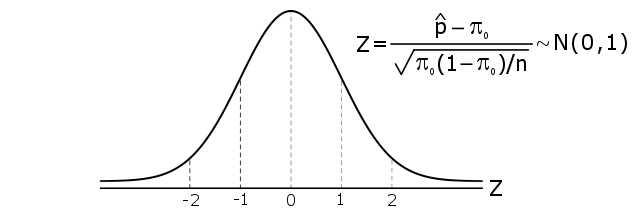 
Een kleine letter #z# wordt gebruikt om de gemeten waarde van #Z# te geven nadat de gegevens zijn verzameld.
Het Berekenen van de p-waarde van een Z-toets voor een Populatieproportie met Statistische Software
De berekening van de #p#-waarde van een #Z#-toets voor #\pi# is afhankelijk van de toetsingsrichting en kan worden berekend met behulp van Excel of R.
Om de #p#-waarde te berekenen van een #Z#-toets voor #\pi# in Excel, gebruik je een van de volgende functies:
\[\begin{array}{lllll}
\phantom{0}\text{Richting}&\phantom{0000}H_0&\phantom{0000}H_a&\phantom{000}p\text{-waarde}&\phantom{0000000000}\text{Excel Functie}\\
\hline
\text{Tweezijdig}&H_0:\pi = \pi_0&H_a:\pi \neq \pi_0&2\cdot \mathbb{P}(Z\geq |z|)&=2 \text{ * }(1 \text{ - }\text{NORM.DIST}(\text{ABS}(z),0,1,1))\\
\text{Linkszijdig}&H_0:\pi \geq \pi_0&H_a:\pi \lt \pi_0&\mathbb{P}(Z\leq z)&=\text{NORM.DIST}(z,0,1,1)\\
\text{Rechtszijdig}&H_0:\pi \leq \pi_0&H_a:\pi \gt \pi_0&\mathbb{P}(Z\geq z)&=1 \text{ - }\text{NORM.DIST}(z,0,1,1)\\
\end{array}\]
Om de #p#-waarde te berekenen van een #Z#-toets voor #\pi# in R, gebruik je een van de volgende functies:
#\begin{array}{lllll}
\phantom{0}\text{Richting}&\phantom{0000}H_0&\phantom{0000}H_a&\phantom{000}p\text{-waarde}&\phantom{000000}\text{R Functie}\\
\hline
\text{Tweezijdig}&H_0:\pi = \pi_0&H_a:\pi \neq \pi_0&2\cdot \mathbb{P}(Z\geq |z|)&2 \text{ * }\text{pnorm}(\text{abs}(z),0,1, \text{FALSE})\\
\text{Linkszijdig}&H_0:\pi \geq \pi_0&H_a:\pi \lt \pi_0&\mathbb{P}(Z\leq z)&\text{pnorm}(z,0,1, \text{TRUE})\\
\text{Rechtszijdig}&H_0:\pi \leq \pi_0&H_a:\pi \gt \pi_0&\mathbb{P}(Z\geq z)&\text{pnorm}(z,0,1, \text{FALSE})\\
\end{array}#
Als #p \leq \alpha#, verwerpen we #H_0# en concluderen we #H_a#. Anders verwerpen we #H_0# niet.
Opmerking: #|z|# geeft de absolute waarde van #z#, namelijk de afstand van #z# tot #0#, ongeacht of #z < 0# of #z > 0#.
Om deze bewering te testen, ondervraagt een journalist die bij een krant werkt #150# burgers met behulp van willekeurige steekproeven. Laat #X# het aantal burgers aangeven dat vóór de nieuwe wet is.
De journalist is van plan een hypothesetest te gebruiken om te bepalen of het aandeel burgers dat vóór de nieuwe wet is, significant verschilt van #0.60#, op het significantieniveau van #\alpha = 0.04#.
Uit de onderzoeksresultaten blijkt dat #106# van de burgers in de steekproef vóór het nieuwe voorstel is.
Bereken de #p#-waarde van de toets en neem een beslissing over #H_0: \pi = 0.60#. Rond je antwoord af op #4# decimalen.
Op basis van deze #p#-waarde, wordt #H_0# wel verworpen, omdat #\,p# #\lt# #\alpha#.
Er zijn een aantal verschillende manieren waarop we de #p#-waarde van de test kunnen berekenen. Klik op een van de panelen om naar een specifieke oplossing te gaan.
Een steekproefgrootte van #150# wordt als groot genoeg beschouwd om de Centrale limietstelling toe te passen. Dit betekent dat de teststatistiek
\[Z=\cfrac{\hat{p} - \pi_0}{\sqrt{\pi_0 \cdot (1-\pi_0) / n}}\]
bij benadering de #N(0,1)# verdeling heeft onder de aanname dat #H_0# waar is.
Bereken de steekproefproportie #\hat{p}#:
\[\hat{p} = \cfrac{X}{n} = \cfrac{106}{150} = 0.70667\]
Bereken de waarde van teststatistiek #z#:
\[z = \cfrac{\hat{p} - \pi_0}{\sqrt{\pi_0\cdot(1-\pi_0)/n}} = \cfrac{0.70667 - 0.60}{\sqrt{0.60\cdot(1 - 0.60) / 150}} = 2.66667\]
Voor een tweezijdige #Z#-test, wordt de #p#-waarde gedefinieerd als zijnde #2\cdot \mathbb{P}(Z \geq |z|)#. Om deze waarde in Excel te berekenen, gebruik je de volgende functie:
NORM.DIST(x, mean, standard_dev, cumulative)
- x: De waarde waarin je de verdelingsfunctie wilt evalueren.
- mean: Het gemiddelde van de verdeling.
- standard_dev: De standaardafwijking van de verdeling.
- cumulative: Een logische waarde die de vorm van de functie bepaalt.
- WAAR - gebruikt de cumulatieve verdelingsfunctie, #\mathbb{P}(X \leq x)#
- ONWAAR - gebruikt de kansdichtheidsfunctie
Dus om #p = 2\cdot \mathbb{P}(Z \geq |z|)# te berekenen, voer je het volgende command uit:
\[
=2 \text{ * }(1 \text{ - } \text{NORM.DIST}(\text{ABS}(z),0,1,1))\\
\downarrow\\
=2 \text{ * }(1 \text{ - } \text{NORM.DIST}(\text{ABS}(2.66667),0,1,1))
\]
Dit geeft:
\[p = 0.0077\]
Aangezien #\,p# #\lt# #\alpha#, moet #H_0: \pi = 0.60# wel worden verworpen.
Een steekproefgrootte van #150# wordt groot genoeg geacht om de Centrale limietstelling toe te passen. Dit betekent dat de teststatistiek
\[Z=\cfrac{\hat{p} - \pi_0}{\sqrt{\pi_0 \cdot (1-\pi_0) / n}}\]
bij benadering de #N(0,1)# verdeling heeft onder de aanname dat #H_0# waar is.
Bereken de steekproefproportie #\hat{p}#:
\[\hat{p} = \cfrac{X}{n} = \cfrac{106}{150} = 0.70667\]
Bereken de waarde van teststatistiek #z#:
\[z = \cfrac{\hat{p} - \pi_0}{\sqrt{\pi_0\cdot(1-\pi_0)/n}} = \cfrac{0.70667 - 0.60}{\sqrt{0.60\cdot(1 - 0.60) / 150}} = 2.66667\]
Voor een twozijdige #Z#-test, wordt de #p#-waarde gedefinieerd als zijnde #2\cdot \mathbb{P}(Z \geq |z|)#. Om deze waarde in R te berekenen, gebruik je de volgende functie:
pnorm(q, mean, sd, lower.tail)
- q: De waarde waarin je de verdelingsfunctie wilt evalueren.
- mean: Het gemiddelde van de verdeling.
- sd: De standaardafwijking van de verdeling.
- lower.tail: Indien WAAR (standaard) geldt, zijn de kansen #\mathbb{P}(X \leq x)#, anders #\mathbb{P}(X \gt x)#.
Dus om #p = 2\cdot \mathbb{P}(Z \geq |z|)# te berekenen, voer je het volgende command uit:
\[
2 \text{ * } \text{pnorm}(q = \text{abs}(z), mean = 0, sd = 1,lower.tail = \text{ONWAAR})\\
\downarrow\\
2\text{ * } \text{pnorm}(q = \text{abs}(2.66667), mean = 0, sd = 1,lower.tail = \text{ONWAAR})
\]
Dit geeft:
\[p = 0.0077\]
Aangezien #\,p# #\lt# #\alpha#, moet #H_0: \pi = 0.60# wel worden verworpen.
omptest.org als je een OMPT examen moet maken.
