Enkelvoudige variantieanalyse: hypothesen en logica

Hoofdstuk 10: Variantieanalyse: Enkelvoudige variantieanalyse

Enkelvoudige variantieanalyse: hypothesen en logica

Doel van enkelvoudige variantieanalyse
De enkelvoudige variantieanalyse (enkelvoudige ANOVA) wordt gebruikt om te testen of de gemiddelde waarden van een continue variabele verschillen tussen drie of meer populaties die worden gedefinieerd door een enkele categorische factor.

Over het algemeen heeft de factor #I# niveaus. Het populatiegemiddelde van de uitkomstvariabele #Y# voor niveau #i# is #\mu_i#, voor #i = 1,...,I#.

Hypothesen van enkelvoudige variantieanalyse
De hypothesen van een enkelvoudige ANOVA zijn als volgt:

#H_0#	#:#	Het populatiegemiddelde voor de uitkomstvariabele is hetzelfde voor alle #I# populaties. #(\mu_1 = \mu_2 = \dots = \mu_I)#
		# \ #
#H_1#	#:#	Ten minste één populatiegemiddelde verschilt van een ander populatiegemiddelde. #(\mu _i \neq \mu _j# voor ten minste één paar niveaus #(i,j))#

Houd er rekening mee dat de alternatieve hypothese van een enkelvoudige ANOVA niet specificeert welke populatiegemiddelden verschillend zouden moeten zijn. Het resultaat van een enkelvoudige ANOVA vertelt je dus alleen of er een significant verschil is tussen de gemiddelden, maar niet welke gemiddelden verschillen.

Als de nulhypothese van een enkelvoudige ANOVA wordt verworpen, moet er een post hoc-toets worden uitgevoerd om te bepalen welke populatiegemiddelden verschillend zijn.

Beschouw een experiment met één factor waarin de uitkomstvariabele de verandering in de systolische bloeddruk is, en de factor het type videoclip dat wordt bekeken.

Stel dat er vijf niveaus (categorieën) zijn voor deze factor: het basisniveau, dat een neutrale videoclip weergeeft, en vier andere niveaus die overeenkomen met verschillende videoclips die één van de vier verschillende intense actiescènes tonen: een autoachtervolging, een zwaardgevecht, skiën op een zwarte piste, en een bokswedstrijd.

De onderzoeksvraag is of het type videoclip dat wordt bekeken enige invloed heeft op de bloeddruk binnen bepaalde populaties. Met andere woorden: is de gemiddelde verandering in de systolische bloeddruk hetzelfde, ongeacht welke videoclip wordt bekeken?

De enkelvoudige ANOVA die we zouden gebruiken om deze onderzoeksvraag te beantwoorden zou de volgende hypothesen hebben:

#H_0#	#:#	Het type videoclip dat wordt bekeken, heeft geen effect. Dat wil zeggen, de gemiddelde verandering in de systolische bloeddruk is hetzelfde voor alle #5# groepen. #(\mu_{neutraal} = \mu_{auto} = \mu_{zwaard} = \mu_{ski} = \mu_{boksen})#
		# \ #
#H_1#	#:#	Het type videoclip dat wordt bekeken, heeft wel een effect. Dat wil zeggen, tenminste één groep heeft een gemiddelde verandering in systolische bloeddruk die verschilt van die van een andere groep. #(\mu_i \neq \mu_j# voor ten minste één paar video's#)#

Om uit te leggen hoe de ANOVA-procedure in staat is om gelijktijdig de gelijkheid van alle populatiegemiddelden te testen met behulp van slechts één enkele toets, moet een tweede type gemiddelde worden geïntroduceerd.

Algemeen populatiegemiddelde
Het algemene populatiegemiddelde #\mu# is het gemiddelde voor de uitkomstvariabele #Y# op alle niveaus van de factor en wordt berekend als het gewogen gemiddelde van de populatiegemiddelden:
\[\mu = \cfrac{\displaystyle\sum_{i = 1}^I N_i\mu_i}{N}\] waarbij #N_i# het aantal individuen is dat tot populatie #i# behoort en #N# het totale aantal individuen in alle populaties.

Stel dat we een continue variabele #Y# hebben die we meten in drie populaties:

Populatie #1# heeft #N_1=100# leden en een gemiddelde van #\mu_1 = 10#.
Populatie #2# heeft #N_2=200# leden en een gemiddelde van #\mu_2 = 20#.
Populatie #3# heeft #N_3=300# leden en een gemiddelde van #\mu_3 = 30#.

In dat geval is het algemene populatiegemiddelde #\mu# :
\[\begin{array}{rcl}
\mu &=& \cfrac{\displaystyle\sum_{i = 1}^I N_i\mu_i}{N}\\\\
&=& \cfrac{100\cdot 10 + 200 \cdot 20 + 300 \cdot 30}{100+200+300}\\\\
&\approx& 23.3
\end{array}\]

Om te testen of alle populatiegemiddelden gelijk zijn, maakt de ANOVA-procedure gebruik van een eenvoudig, maar krachtig stukje logica: als de nulhypothese waar is en alle populatiegemiddelden gelijk zijn, dan zijn de populatiegemiddelden ook gelijk aan het algemene populatiegemiddelde.

\[\text{Als }\mu_1 = \mu_2 = \ldots = \mu_I\text{,}\\\text{dan }\mu_i = \mu,\text{ voor }i = 1,\ldots,I\] Een andere manier om over deze stelling na te denken, is dat als alle populatiegemiddelden gelijk zijn, we de drie populaties kunnen beschouwen als één grote populatie met één algemeen gemiddelde.

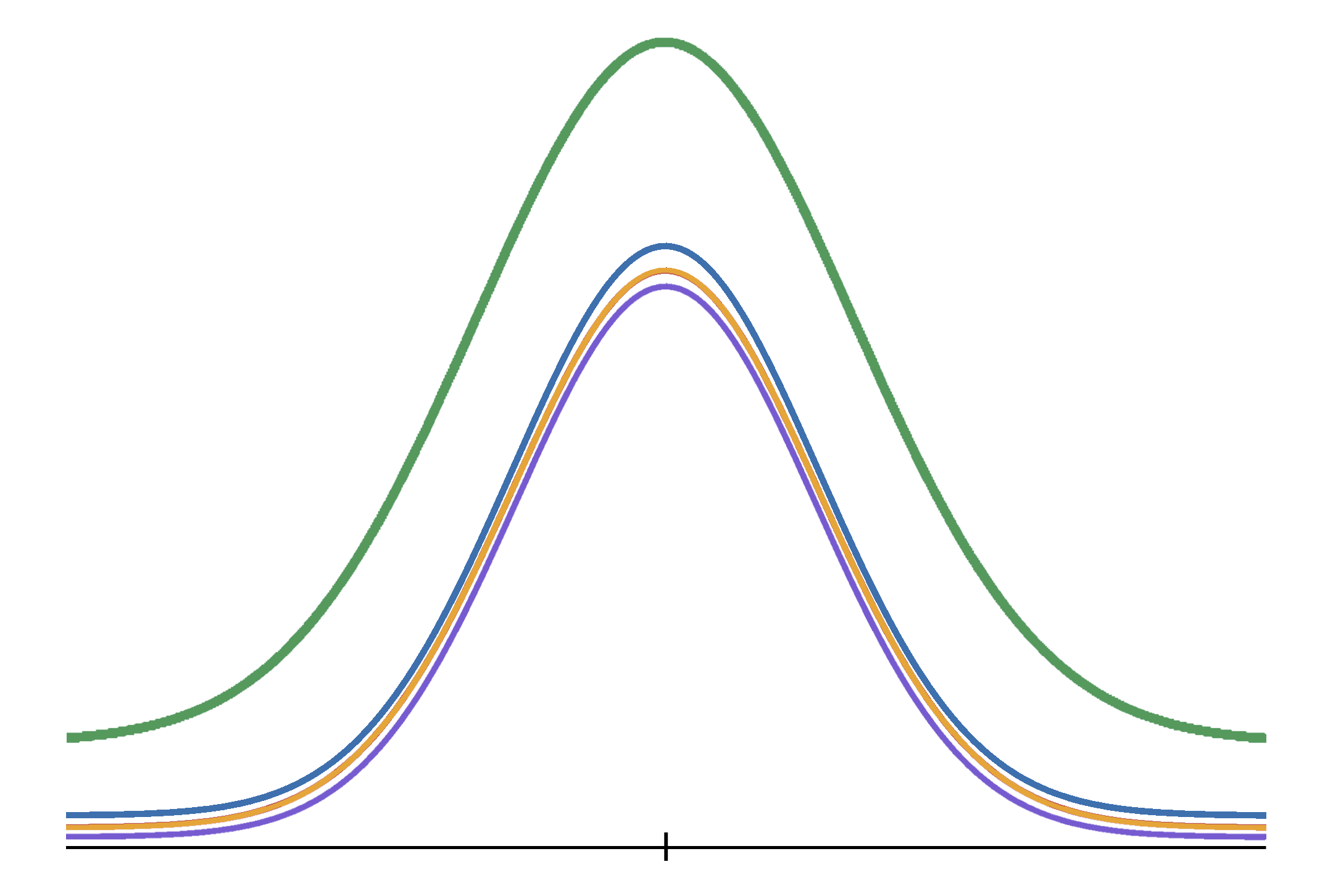#\orange{\mu_1} =\purple{\mu_2} = \blue{\mu_3} = \green{\mu}#

Als de nulhypothese echter onjuist is, is het tegenovergestelde waar: als de populatiegemiddelden niet allemaal gelijk zijn, zal ten minste één populatiegemiddelde verschillen van het algemene populatiegemiddelde.

We kunnen dus een idee krijgen van het verschil tussen de populatiegemiddelden door de gemiddelde afstand tussen de populatiegemiddelden en het algemene populatiegemiddelde te beschouwen.

De onderstaande afbeeldingen laten zien hoe de gemiddelde afstand tussen de populatiegemiddelden #(\orange{\mu_1}, \purple{\mu_2}, \blue{\mu_3} )# en het algemene populatiegemiddelde #(\green{\mu})# toeneemt naarmate het verschil tussen de populatiegemiddelden groter wordt.

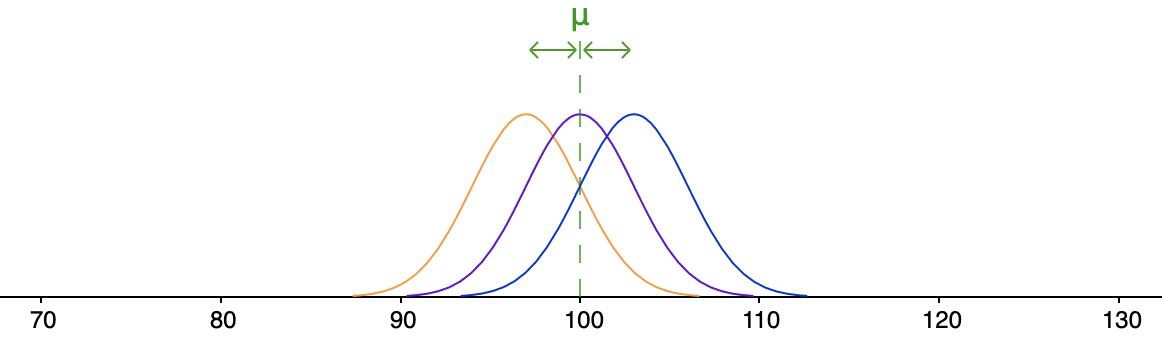
\[\begin{array}{rcl}
\text{gemiddelde afstand}&=&\cfrac{|\orange{97}-\green{100}|+|\purple{100}-\green{100}|+|\blue{103}-\green{100}|}{3}\\\\
&=&\cfrac{\orange{3}+\purple{0}+\blue{3}}{3}\\\\
&=& 2
\end{array}\]

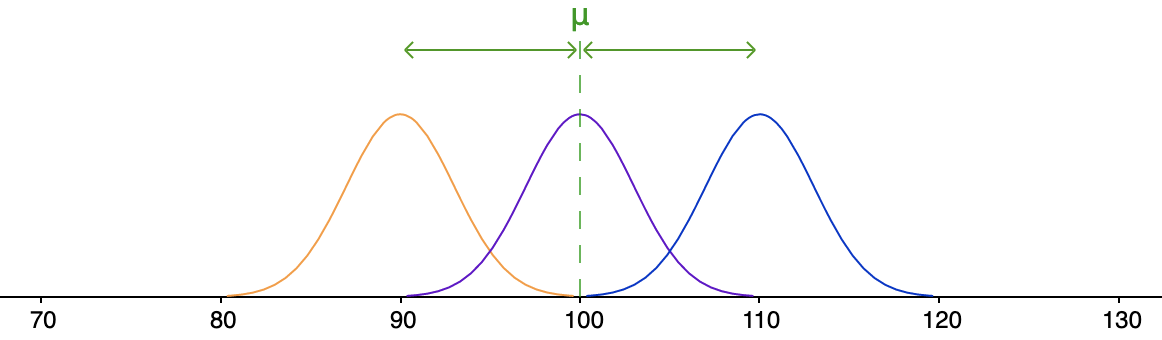
\[\begin{array}{rcl}
\text{gemiddelde afstand}&=&\cfrac{|\orange{90}-\green{100}|+|\purple{100}-\green{100}|+|\blue{110}-\green{100}|}{3}\\\\
&=&\cfrac{\orange{10}+\purple{0}+\blue{10}}{3}\\\\
&\approx& 6.7
\end{array}\]

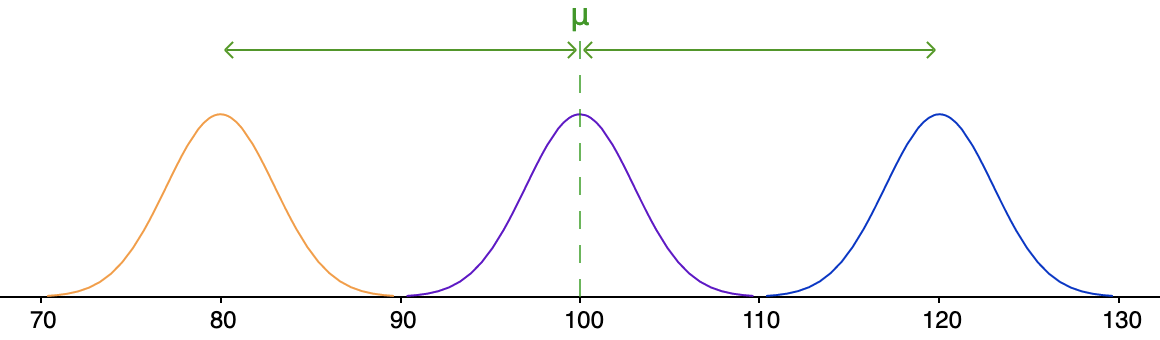
\[\begin{array}{rcl}
\text{gemiddelde afstand}&=&\cfrac{|\orange{80}-\green{100}|+|\purple{100}-\green{100}|+|\blue{120}-\green{100}|}{3}\\\\
&=&\cfrac{\orange{20}+\purple{0}+\blue{20}}{3}\\\\
&\approx& 13.3
\end{array}\]

Er zit echter een addertje onder het gras. Omdat we willekeurige steekproeven uit de populaties moeten trekken om een schatting te krijgen van de populatiegemiddelden en het algemene populatiegemiddelde, is er een tweede factor waar we rekening mee moeten houden, namelijk de variabiliteit binnen elke populatie.

Als de variabiliteit binnen de populaties laag is en de individuele verschillen tussen de leden van elke populatie klein zijn, dan is de kans groot dat we een goede schatting kunnen krijgen van de populatiegemiddelden.

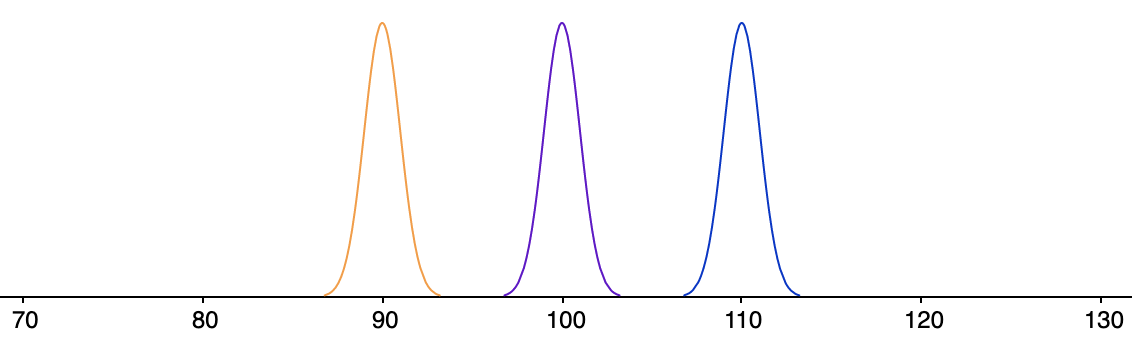
Dit geeft ons vertrouwen in het interpreteren van de geschatte verschillen tussen de populatiegemiddelden en het algemene populatiegemiddelde als bewijs tegen onze nulhypothese.

Naarmate de variabiliteit binnen de populatie toeneemt, is een voorzichtigere aanpak op zijn plaats. Meer variabiliteit betekent meer onzekerheid, en meer onzekerheid betekent dat we meer bewijs nodig hebben om de nulhypothese te kunnen verwerpen.

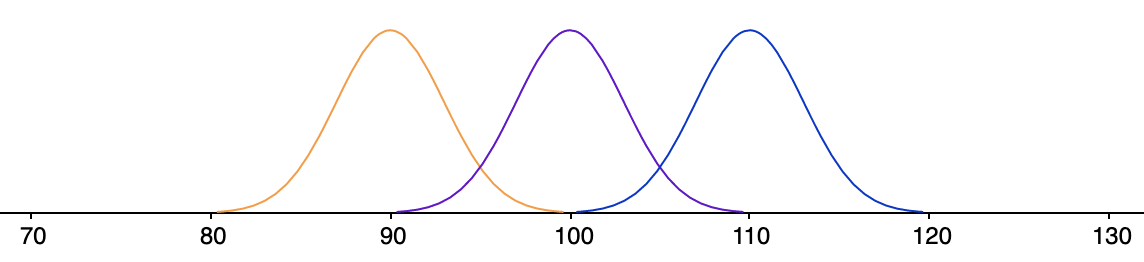
In de meest extreme gevallen is de variabiliteit zo groot dat we ernstige fouten zouden kunnen maken als we bij de beslissing om de nulhypothese al dan niet te verwerpen alleen maar rekening zouden houden met de gemiddelde afstand tussen de populatiegemiddelden en het algemene populatiegemiddelde.

Logica achter de procedure van de variantieanalyse
In de ANOVA-procedure wordt de sterkte van het bewijs tegen de nulhypothese van gelijke populatiegemiddelden bepaald door twee factoren:

Het geschatte gemiddelde verschil tussen de populatiegemiddelden #\mu_i# en het algemene populatiegemiddelde #\mu#.
- Naarmate de geschatte gemiddelde afstand toeneemt, neemt ook de kracht van het bewijs tegen de nulhypothese toe.
De geschatte variabiliteit binnen de populaties.
- Naarmate de geschatte variabiliteit toeneemt, neemt de kracht van het bewijs tegen de nulhypothese af.

Gebruik de onderstaande interactieve grafiek om een idee te krijgen van de interactie tussen deze twee factoren. De schuifregelaars voor de gemiddelden bepalen de posities van de verdelingen, terwijl de schuifregelaar voor de variabiliteit de vorm van de verdelingen regelt.

De #\green{\text{groene lijn}}# geeft de positie van het algemene populatiegemiddelde aan.

De #\red{\text{rode balk}}# geeft aan hoe sterk het bewijs tegen de nulhypothese waarschijnlijk zal zijn als we willekeurige steekproeven zouden trekken uit elk van de populaties.

ANOVA Logic Interactive