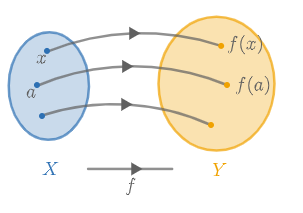
Laat #\blue X# en #\orange Y# verzamelingen zijn.
Een functie #f# van #\blue X# naar #\orange Y# wijst aan elk element #x# uit #\blue X# één element uit #\orange Y# toe. Dit element noteren we met #{f(x)}#.
De notatie #f : \blue X \to \orange Y# geeft aan dat #f# een functie is van #\blue X# naar #\orange Y#.
We noemen #f(x)# de functiewaarde (of kort gezegd: waarde) van #f# in #x#. Dit wordt ook wel het beeld van origineel #x# onder #f# genoemd.
Een functie kunnen we zien als een soort machine. We stoppen een element #x# van #\blue X# in de machine en vervolgens komt er aan de andere kant van de machine een element #f(x)# van #\orange Y# uit de machine. De machine berekent #f(x)# volgens een door #f# vastgelegde regel.
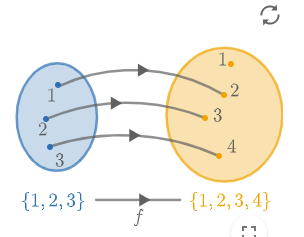
Rechts staat een voorbeeld van #f: \blue{\{1,2,3\}} \to \orange{\{1,2,3,4\}}#.
We kunnen de functie #f# noteren als een rijtje getallen, namelijk #[2,3,4]#.
Dit betekent:
\[f(1)=2\]
\[f(2)=3\]
\[f(3)=4\]
Een functie is eigenlijk een bijzondere vorm van een relatie, zoals gedefinieerd bij verzamelingen. Want een functie is eigenlijk een relatie tussen verzameling #\blue X# en #\orange Y#. Hierbij is een element #x# uit #\blue X# gerelateerd aan precies één element uit #\orange Y#. Dit element noteren we met #f(x)#.
Een functie noteren we vaak met de letter #f#, van functie. Wanneer we echter ook een tweede functies willen opschrijven, kunnen we niet nog een keer de letter #f# gebruiken. Deze is al bezet. We gebruiken vaak de letter #g# voor de eerstvolgende functie. Wanneer we hierna meer functies willen opschrijven gebruiken we vaak de volgende letter uit het alfabet.
Hierbij is ook toegestaan om bijvoorbeeld letters uit het Griekse alfabet te gebruiken, zoals #\alpha#, #\phi# of #\rho#. We mogen zelfs meerdere letters gebruiken, zoals een afkorting.
In het algemeen houden we het graag zo kort mogelijk en schrijven we bijvoorbeeld #T# voor temperatuur en niet #Temp# of #Temperatuur#.
We kunnen functies op verschillende manieren representeren. Eén van de meest gebruikte manieren hiervoor is het functievoorschrift.
Een functievoorschrift voor een functie #f# is een expliciete uitdrukking om weer te geven wat de functie precies doet.
We noteren dit als: #f(\blue x)=\ldots#, waarbij op de puntjes een uitdrukking met variabele #\blue x# staat. Deze algebraïsche uitdrukking vertelt precies wat de functie #f# doet.
In het functievoorschrift is niet te zien uit welke verzamelingen #\blue x# en #f(\blue x)# komen. Vaak is het impliciet duidelijk dat #\blue x# een reëel getal is. Hier komen we bij domein en bereik op terug.
Voorbeelden
\[\begin{array}{rcl}f(\blue x)&=&\blue x^2 \\ \\ g(\blue x)&=&\sqrt{\blue x} \\ \\ h(\blue x)&=&\blue x^3+\blue x+1 \end{array}\]
Met behulp van het functievoorschrift kunnen we de functiewaarde van een element gemakkelijk berekenen.
Bekijk de functie hiernaast. Als we de functiewaarde in #\blue x=\blue2# willen uitrekenen, volgen we het functievoorschrift. Merk op dat we alle #\blue x#'en die we tegenkomen vervangen door een #\blue2#. We noemen dit substitueren.
Dus de functiewaarde van #\blue x=\blue2# is gelijk aan #4#. We noteren de functiewaarde van #\blue x\blue=2# met #f(\blue2)#. Dus #f(\blue2)=4#.
Op een soortgelijke manier vinden we dat de functiewaarde van #\blue x=\blue{-4}# gelijk is aan #16#. Ofwel #f(\blue{-4}) = 16#.
Voorbeelden
\[\begin{array}{rclcl} \text{Als } f(\blue x)&=&\blue x^2 &\text{ dan }&\\ \\f(\blue2)&=&\blue2^2&=&4 \\ \\&&\text{en}&& \\ \\f(\blue{-4})&=&\left(\blue{-4} \right)^2&=&16\end{array}\]
Hierboven zagen we dat we een functie kunnen weergeven met een functievoorschrift van de vorm #f(\blue x)=\ldots#, waarbij op de puntjes staat wat de functie doet.
Wiskundigen zelf gebruiken vaak de "pijltjesnotatie". Deze ziet er als volgt uit:
\[f : \blue x \mapsto \ldots\]
Ook hierbij staat op de puntjes wat de functie doet. De functiewaarde voor een element #\blue x# wordt nog steeds genoteerd met #f(\blue x)#. Op deze manier wordt er onderscheid gemaakt tussen de functiewaarde en de functie zelf.
De reden dat wiskundigen de pijltjesnotatie gebruiken is onder andere om duidelijk verschil te maken tussen een functie, een vergelijking en de functiewaarde. In de praktijk is dit verschil vaak duidelijk uit de context en kan er geen verwarring ontstaan. In deze cursus gebruiken we de korte notatie #f(\blue x)=\ldots#.
We gebruiken in deze cursus wel de notatie #f : X \to Y#, die gebruikt wordt om te laten zien van welke verzameling naar welke verzameling de functie gaat. De onderste voorbeelden rechts laten zien hoe de officiële notatie eruit ziet als ook de verzamelingen waartussen een functie loopt, wordt weergegeven.
Voorbeelden
\[\begin{array}{c}f :\blue x \mapsto \blue x^2 \\ \\ \\ g :\blue x \mapsto \sqrt{\blue x} \\ \\ \\ h : \blue x \mapsto \blue x^3+\blue x+1 \\ \\ \\ \\ f : \mathbb{R} \to \mathbb{R} : \blue x \mapsto \blue x^2 \\ \\ \\ g : \ivco{0}{\infty} \to \ivco{0}{\infty} :\blue x \mapsto \sqrt{\blue x} \\ \\ \\ h : \mathbb{R} \to \mathbb{R} : \blue x \mapsto \blue x^3+\blue x+1 \end{array}\]
Het lijkt nu alsof een functievoorschrift er altijd uit ziet als #f(\blue x) = \blue x^2# of #f(\blue x) = 2\cdot \blue x +3# of iets anders vergelijkbaars. Dit is echter niet altijd het geval.
Een functie kan ook verschillende situaties onderscheiden. In dat geval geldt voor bepaalde waarden van #\blue x# de ene uitdrukking en voor andere waarden van #\blue x# een andere uitdrukking.
In de voorbeelden rechts staat de absolute waarde functie, die voor #\blue x \lt0# gelijk is aan #-\blue x# en voor #\blue x \geq 0# aan #\blue x#.
Dat betekent bijvoorbeeld #f(\blue{-2})=2#, maar #f(\blue3)=3#.
Ook dit is een functievoorschrift, want het vertelt voor elk getal #\blue x# hoe de functiewaarde uitgerekend wordt. Een functie van deze vorm noemen we stuksgewijs gedefinieerd.
Voorbeelden
Absolute waarde functie:
\[f(\blue x)=\left\{\begin{array}{ll}-\blue x & \text{als } \blue x\lt0, \\ \blue x & \text{als } \blue x \geq 0.\end{array}\right.\]
De absolute waarde functie noteren we vaak met #f(\blue x)=|\blue x|#.
Deltafunctie:
\[\delta_a(\blue x)=\left\{\begin{array}{ll}1 & \text{als } \blue x=a ,\\ 0 & \text{als } \blue x \ne a.\end{array}\right.\]
Een functievoorschrift #f(\blue x) = \ldots# wordt vaak genoteerd met #\orange y = \ldots#. Dit betekent hetzelfde. Het voordeel hiervan is dat een functievoorschrift korter wordt. Een nadeel is dat we nu moeilijker onderscheid kunnen maken tussen twee functies.
De twee functievoorschriften #f(\blue x) = \blue x^2# en #h(\blue x) = \blue x^3 +\blue x +1# stellen duidelijk verschillende functies voor. Wanneer we deze echter schrijven als #\orange y= \blue x^2# en #\orange y = \blue x^3 + \blue x + 1# lijkt het alsof de #\orange y# twee verschillende dingen betekent.
Het gebruik van de letters #\blue x# en #\orange y# is een gewoonte. We zouden net zo goed van #a# en #b# kunnen gebruiken. Zo betekenen #\orange y = \blue x^2# en #b = a^2# vaak hetzelfde.
Voorbeelden
\[\begin{array}{rcl}\orange y&=&\blue x^2 \\ \\ \\ \orange y&=&\sqrt{\blue x} \\ \\ \\ \orange y&=& \blue x^3+ \blue x+1 \end{array}\]
We gebruiken in een functievoorschrift vaak de letter #\blue x#, maar dat is niet verplicht. We mogen ook andere letters gebruiken. Zo wordt #\blue t# vaak gebruikt als we een functie hebben die over tijd gaat. Het functievoorschrift ziet er dan uit als:
\[f(\blue t)=\ldots\]
Hierbij staat op de puntjes een uitdrukking met #\blue t#.
Voorbeelden
\[\begin{array}{rcl}f(\blue t)&=&\blue t^2 \\ \\ g(\blue t)&=&\sqrt{\blue t} \\ \\ h(\blue t)&=& \blue t^3+ \blue t+1 \end{array}\]
Bekijk de functie:
\[f(x)=-9 x \]
Bereken de functiewaarde bij #3#.
De functiewaarde bij #3# is: #-27#
Om de functiewaarde bij #3# te berekenen, substitueren we #x=3# in de functie.
We krijgen dan: \[f(3)=\left(-9\right)\cdot 3=-27\]
Dus de functiewaarde bij #3# is #-27#.
 Het begrip functie
Het begrip functie