Functies: Functies
Het bereik van een functie
De waarden die een functie #f:\blue X\to \orange Y# aanneemt liggen in het codomein #\orange{Y}#. Niet ieder element uit het codomein #\orange{Y}# hoeft echter voor te komen als een functiewaarde van #f#, zoals duidelijk is in het volgende voorbeeld.
|
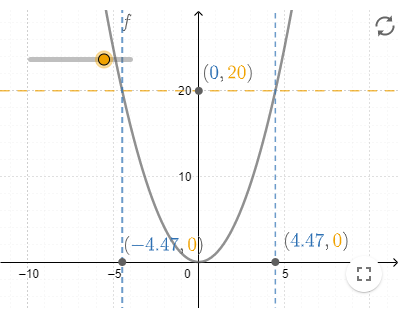
De functie #f: \blue{\mathbb{R}} \to \orange{\mathbb{R}}# met functievoorschrift #f(x)=x^2# heeft als minimumwaarde #f(0)=0# en kan verder alle waarden groter dan #0# aannemen. Dus alle waarden in het interval #\ivco{0}{\infty}# worden door #f# bereikt. We noemen #\ivco{0}{\infty}# het bereik van #f#. In de grafiek is te zien dat de horizontale lijn #y=\orange a# precies dan snijpunten met de grafiek heeft als #\orange a# in het bereik van #f# ligt. |
 |
We geven nu de formele definitie van het bereik van een functie #f#.
Bereik
Van een functie #f: \blue X \to \orange Y# heet #\orange Y# het codomein.
De verzameling van alle functiewaarden #f(x)# in #\orange Y# voor #x \in \blue X# heet het bereik van #f#.
Als het bereik gelijk is aan #\orange Y#, dan noemen we #f# surjectief.
Voorbeeld
Van #f: \blue{\mathbb{R}} \to \orange{\mathbb{R}}#
met functievoorschrift #f(x)=-x^2#
is het bereik #\ivoc{-\infty}{0}#
Want een punt #y# ligt in het bereik van #f# dan en slechts dan als de vergelijking #y = -{{2}\over{x-3}}# een oplossing in #x# heeft.
Voor #y \neq 0# geldt
\[\begin{array}{rcl}
y &=&\displaystyle -{{2}\over{x-3}}\\
&&\phantom{xxx}\blue{\text{gegeven functie}}\\
y(x-3)&=& -2\\
&&\phantom{xxx}\blue{\text{beide kanten met }x-3\text{ vermenigvuldigd} }\\
x-3 &=& \dfrac{-2}{y}\\
&&\phantom{xxx}\blue{\text{gedeeld door }y \text{ (merk op }y\ne 0\text{)}} \\
x &=&\displaystyle \frac{-2}{y}+3\\
&&\phantom{xxx}\blue{\text{aan beide kanten } 3 \text{ opgeteld}}
\end{array}\]
Voor #y=0# geldt
\[ \begin{array}{rcl}
0 &=&\displaystyle -{{2}\over{x-3}}\\
&&\phantom{xxx}\blue{y=0\text{ ingevuld in functie}}\\
0(x-3)&=& -2\\
&&\phantom{xxx}\blue{\text{beide kanten met }x-3\text{ vermenigvuldigd} }\\
0&=& -2\\
&&\phantom{xxx}\blue{\text{uitgerekend}}
\end{array}\]
We concluderen:
- Voor elke #y\ne0# heeft de vergelijking #y = -{{2}\over{x-3}}# wel een oplossing in #x#, namelijk #x=3-{{2}\over{y}}#.
- Voor #y=0# wordt de vergelijking #0= -{{2}\over{x-3}}#; deze heeft geen reële oplossing.
omptest.org als je een OMPT examen moet maken.
