Basisvaardigheden algebra: Kwadratische functies
Kwadratische functies en parabolen
We zullen nu kijken naar de eigenschappen van de grafiek van de kwadratische functie #a \cdot x^2+b \cdot x +c#. Daarnaast zullen we kijken naar de snijpunten van de grafieken van twee kwadratische functies.
Een kwadratische functie #f# wordt gegeven door #f(x)=ax^2+bx+c#, waarin #a#, #b# en #c# reële getallen zijn en #a\neq 0#.
De grafiek behorende bij zo'n functie heet een parabool.
Wanneer #a\gt0#, dan spreken we van een dalparabool en bij #a\lt0# van een bergparabool.
De parabool heeft een verticale symmetrie-as: #x=-\frac{b}{2a}#. Spiegelen om deze as door de top laat de grafiek onveranderd.
Als je de grafiek draait in het platte vlak, dan blijft de vorm hetzelfde maar is het niet meer de grafiek van een functie, omdat er verticale lijnen zijn die de parabool twee keer snijden. Als we een willekeurige parabool in het vlak zo draaien dat de symmetrie-as verticaal staat, dan krijgen we de vertrouwde grafiek van een kwadratische functie.
Om de grafiek van een kwadratische functie te onderscheiden van een willekeurige parabool spreken we ook wel van verticale parabool als de symmetrie-as verticaal is.
De betekenis van deze namen wordt duidelijk uit onderstaande grafiek van de dalparabool van #x^2-8# en de bergparabool van #-x^2+8#.
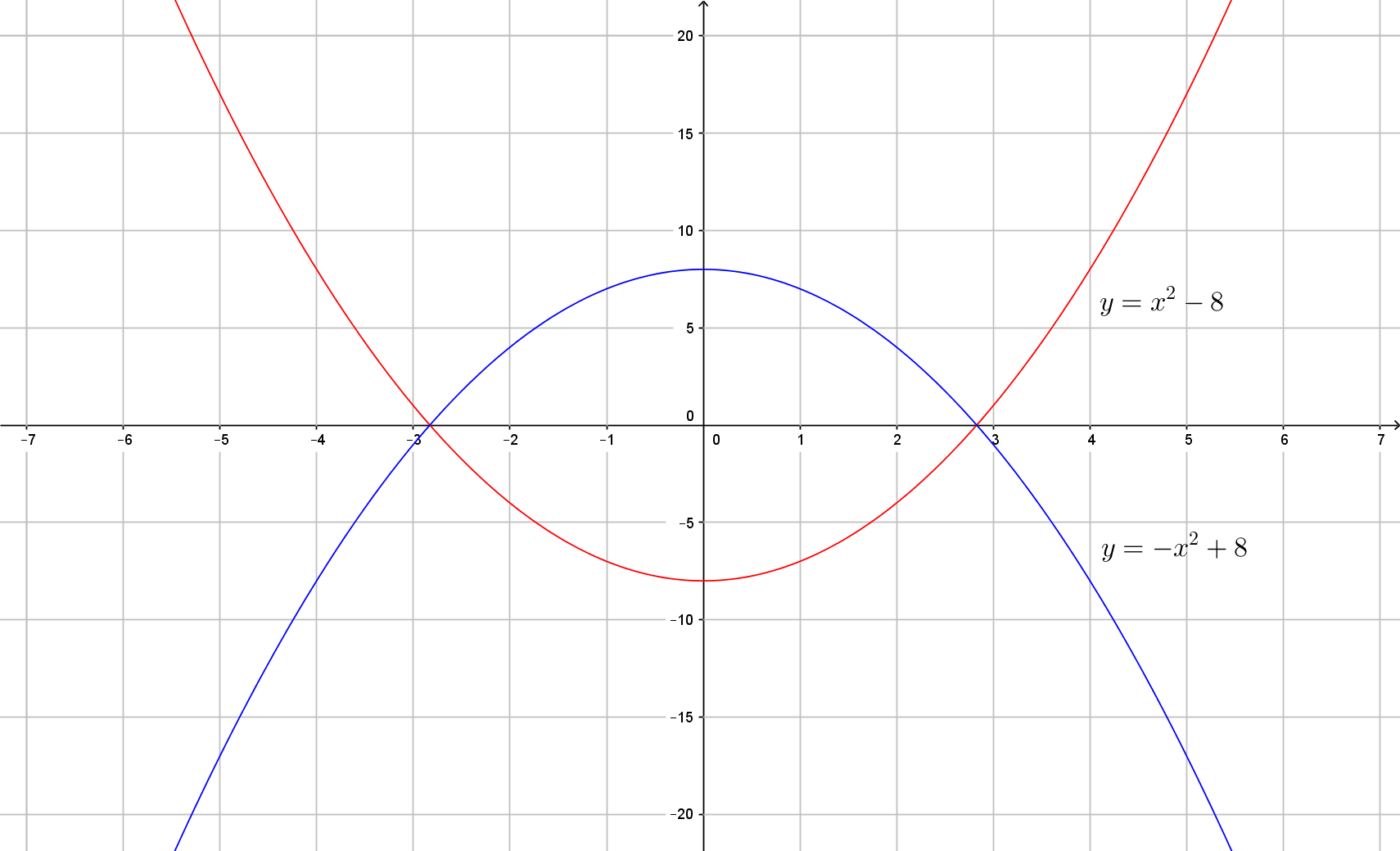
Om te weten te komen wat de nulpunten van een kwadratische functie zijn, moeten we de snijpunten van de parabool met de #x#-as zien te vinden. Dit is het oplossen van een kwadratische vergelijking. De top vinden we door gebruik te maken van de symmetrie-as bij #x=-\frac{b}{2a}#.
Snijdende parabolen
Twee verticale parabolen snijden elkaar in ten hoogste twee punten.
We zullen nu naar enkele voorbeelden van grafieken van kwadratische functies kijken.
De rode punten zijn de vier gevraagde punten. Deze worden als volgt berekend:
De functie is al geschreven in de vorm #a \cdot x^2+b \cdot x +c# met #a =3#, #b=-8# en #c=-25#. Aangezien #a>0#, is de grafiek een dalparabool.
Het snijpunt met de #y#-as is gelijk aan de waarde van de constante in de kwadratische functie, en is dus gelijk aan #-25#. De coördinaten van het snijpunt met de #y#-as zijn dus #\rv{0,-25}#.
De #x#-waarde van de top wordt gegegeven door #x=-\dfrac{b}{2 \cdot a}# en is dus gelijk aan:
\[\begin{array}{rclrl}
x&=& -\dfrac{-8}{2 \cdot 3} &&\phantom{xxx}\color{blue}{\text{formule ingevuld}}\\
&=& {{4}\over{3}} &&\phantom{xxx}\color{blue}{\text{vereenvoudigd}}\\
\end{array}\]
De #y#-waarde van de top wordt berekend door #x={{4}\over{3}}# in te vullen in de formule. Dat geeft:
\[\begin{array}{rclrl}
y&=& 3 \cdot {{4}\over{3}}^2 -8 \cdot {{4}\over{3}} -25
&&\phantom{xxx}\color{blue}{\text{formule ingevuld}}\\
&=& \displaystyle -{{91}\over{3}} &&\phantom{xxx}\color{blue}{\text{uitgerekend}}\\
\end{array}\]
De coördinaten van de top zijn dus: #\rv{{{4}\over{3}},-{{91}\over{3}}}#.
.Om de waarden in de grafiek te tekenen, moeten we ze afronden. Dat geeft: .#\rv{1.3,-30.3}#.
De snijpunten met de #x#-as zijn de punten waarvoor geldt #y=0#.
\[\begin{array}{rcl} 3\cdot x^2-8\cdot x-25 &=& 0 \\&&\phantom{xxx}\color{blue}{\text{de op te lossen vergelijking}}\\
x=\dfrac{-{-8}-\sqrt{\left(-8\right)^2-4 \cdot 3 \cdot -25}}{2 \cdot 3} &\lor& x=\dfrac{-{-8}+\sqrt{\left(-8\right)^2-4 \cdot 3 \cdot -25}}{2 \cdot 3} \\&&\phantom{xxx}\color{blue}{\text{abc-formule ingevuld}}\\ \displaystyle x={{4-\sqrt{91}}\over{3}} &\lor& \displaystyle x={{\sqrt{91}+4}\over{3}} \\&&\phantom{xxx}\color{blue}{\text{uitgerekend}}\end{array}\]
De coördinaten van de snijpunten met de #x#-as zijn dus: #\rv{{{4-\sqrt{91}}\over{3}},0}# en #\rv{{{\sqrt{91}+4}\over{3}},0}#.
Om de waarden in de grafiek te tekenen, moeten we ze afronden. Dat geeft: #\rv{-1.8,0}# en #\rv{4.5,0}#.
De volgende vier punten zijn dus de gevraagde punten in de grafiek: #\rv{0,-25}#, #\rv{{{4}\over{3}},-{{91}\over{3}}}#, #\rv{{{4-\sqrt{91}}\over{3}},0}# en #\rv{{{\sqrt{91}+4}\over{3}},0}#.
De gevraagde punten zijn in de figuur verbonden door een vloeiende kromme: de dalparabool gegeven door het functievoorschrift.
omptest.org als je een OMPT examen moet maken.
