Negatieve exponenten

Basisvaardigheden algebra: Negatieve exponenten

Negatieve exponenten

Tot nu toe hebben we zowel lineaire functies en vergelijkingen als kwadratische functies en vergelijkingen gezien. Nu gaan we kijken naar een aantal functies en vergelijkingen met een negatieve exponent. We beginnen met een rekenregel.

Rekenregel voor negatieve machten

Voor onbekende #x# en een getal #n# geldt

\[x^{-n}=\frac{1}{x^n}\]

Dit betekent dat #x^{-1}=\frac{1}{x}# en #x^{-2}=\frac{1}{x^2}#.

Deze regel geldt niet alleen voor functies, maar ook voor getallen. Zo geldt:

\[\frac{1}{2}=2^{-1}\]

Quotiëntfuncties

Het product #(x+2)\cdot(x+3)^{-1}# is gelijk aan de quotiëntfunctie #\frac{x+2}{x+3}#.

In tegenstelling tot lineaire en kwadratische functies zijn functies met een negatieve exponent niet overal gedefinieerd. Dit betekent dat er niet voor elke waarde van #x# een bijbehorende waarde #f(x)# bepaald is. Ter illustratie zullen we kijken naar de functie #\frac{1}{x}#. Daarvoor staat hieronder de grafiek van de functie #y=\frac{1}{x}#.

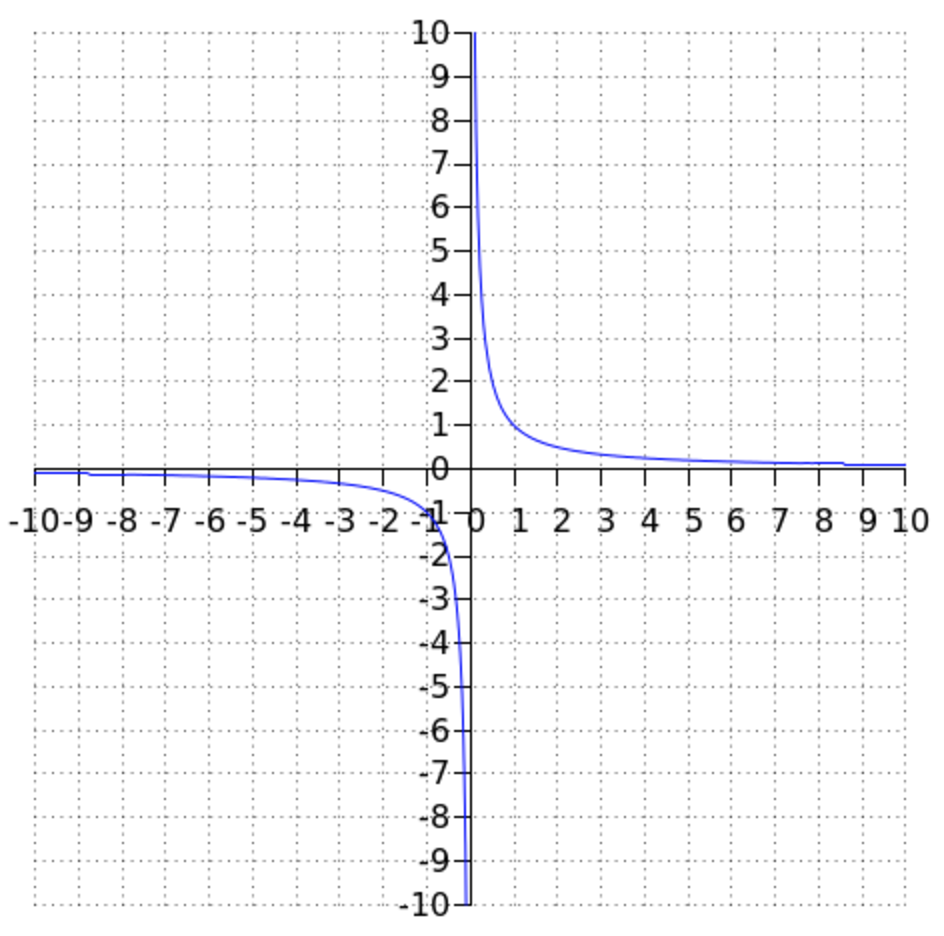
De functie #\frac{1}{x}# is gedefinieerd voor alle reële getallen #x\ne0#. In #x=0# is de noemer gelijk aan #0#, dus de breuk in het functievoorschrift is dan niet gedefinieerd. In de buurt van #x=0# komen de functiewaarden heel ver van #0#:

Hyperbool en asymptoot

Rechts van #x=0# gaat de functie #\frac{1}{x}# naar oneindig (#\infty#); dat wil zeggen: je kunt willekeurig grote getallen als functiewaarde krijgen door #x# maar positief en dicht genoeg bij #0# te kiezen. Net zo gaat de functie links van #x=0# naar min oneindig (#-\infty#). De grafiek van #\frac{1}{x}# komt dus willekeurig dicht bij de #y#-as. Met andere woorden: de #y#-as is een verticale asymptoot van de grafiek (we zeggen ook wel: van de functie).

De #x#-as is een horizontale asymptoot van de grafiek: als we #x# naar oneindig laten gaan, wordt #\dfrac{1}{x}# steeds kleiner en komt de functiewaarde steeds dichter bij #0#. We vinden dus punten van de grafiek die willekeurig dicht bij de #x#-as liggen, maar er niet op liggen. Hetzelfde geldt als we #x# naar min oneindig laten gaan; ook dan komt #\dfrac{1}{x}# steeds dichter bij #0# zonder er gelijk aan te zijn.

De grafiek van #\frac{1}{x}# wordt wel een hyperbool genoemd. Een kenmerk van de hyperbool is het tweetal lijnen waar de grafiek dichter en dichter bij komt zonder ze te snijden. Deze lijnen heten asymptoten.

Orthogonaal

In het algemeen hoeven de asymptoten van een hyperbool niet loodrecht op elkaar te staan, zoals met de grafiek van #\frac{1}{x}# het geval is. Als dit wel zo is, dan noemen we de hyperbool ook wel orthogonaal.

Voorbeeld

We zeggen dat de constante functie #y=4# geen asymptoot heeft: de waarden van de functie liggen willekeurig dicht bij #4#; ze zijn er namelijk gelijk aan. Omdat we bij de definitie van asymptoot uitsluiten dat de waarde gelijk wordt (of, algemener, dat de punten van de grafiek op de asymptoot liggen), is er geen sprake van een asymptoot.

Welke van de onderstaande uitspraken is/zijn waar voor alle reële getallen #x# ongelijk aan #0#

0

De onderstaande uitspraken zijn waar:

#\frac{8}{x}=8\cdot x^{-1}#
#\frac{1}{9 \cdot x^2}=\frac{1}{9} \cdot x^{-2}#

De volgende uitspraken zijn niet waar:

#\frac{1}{9 \cdot x}\ne 9 \cdot x^{-1}#, want #\frac{1}{9 \cdot x}=\frac{1}{9} \cdot x^{-1}#
#\frac{3}{x^2} \ne \frac{1}{3}\cdot x^{-2}#, want #\frac{3}{x^2}=3\cdot x^{-2}#

Nieuw voorbeeld