Bulletlening

Rijen en reeksen: Financiële toepassingen van rijen en reeksen

Bulletlening

De theorie van rijen en reeksen geeft een goed uitgangspunt om verschillende soorten leningen te bespreken. We zullen het hebben over leningen die een looptijd hebben van periodes van vaste lengte, waarbij aan het eind van elke periode een vaste rente betaald wordt over de restschuld. De oorspronkelijke schuld wordt afgelost met aflossingen aan het eind van elke periode.

In de bulletlening, die hieronder aan bod komt, is die aflossing nihil tot de laatste periode. Twee andere vormen, de lineaire lening en de annuïteitenlening, worden later behandeld. We beginnen met een beschrijving van het algemene patroon.

Leningen

Het gaat bij leningen steeds over een looptijd van #n# perioden van vaste lengte (denk aan tijdseenheden als een maand of een jaar), waarbij aan het begin een kapitaal #K# geleend wordt en de schuld inclusief interest aan het einde van de looptijd #n# terugbetaald moet zijn.

De interest noteren we als #p\%#. Ook werken we veel met de groeivoet #i = \frac{p}{100}# in plaats van het percentage #p\%#. Bij de leningen die we behandelen, wordt de rente over de restschuld aan het einde van elke periode betaald.

We gebruiken hierbij de volgende notatie, waarbij #j# een periode aan geeft (dus #j=1,2,\ldots,n#):

#a_j# is de aflossing aan het einde van de #j#-de periode
#r_j# is de rentebetaling aan het einde van de #j#-de periode
#R_j# is de schuldrest aan het einde van de #j#-de periode

De kenmerken zijn:

#R_0=K#
#R_j = R_{j-1}-a_j#
#R_n = 0#
#\sum_{j=1}^na_j =K#
#r_j = R_{j-1}\cdot i#

De formule #R_0=K# drukt uit dat aan het einde van de #0#-de periode, ofwel aan het begin van de lening, de schuldrest gelijk is aan #K#, het beginkapitaal.
Aan het eind van periode #j# is de schuldrest gelijk aan het verschil van de schuld aan het einde van de vorige periode met de aflossing over die periode, dus #R_{j}=R_{j-1}-a_j#.
De formule #R_n=0# drukt uit dat aan het einde van de lening, de schuld is afbetaald.
De som #\sum_{j=1}^na_j# van alle aflossingen is gelijk aan het bedrag dat geleend is: #K#.
Aan het eind van periode #j# moet #p\%# rente betaald worden over de schuld aan het begin van die periode, dus over de schuld, #R_{j-1}#, aan het eind van de vorige periode. Daarom geldt #r_j = \frac{p}{100}\cdot R_{j-1}=i\cdot R_{j-1}#.

Als er voor het einde van de looptijd geen rentebetaling en geen aflossing plaats zou vinden, dan volgt de schuldrest het exponentiële groeimodel: #R_j = K\cdot (1+i)^j# voor #j\lt n#. Deze situatie past alleen in bovenstaand model als er één periode is #(n=1)#, omdat we er hierboven van uit gaan dat er aan het einde van elke periode rente betaald wordt. In dat geval is #i# de rente over de hele periode en is #K-a_1 =R_0-a_1 = R_1=0#, dus #a_1=K# en #r_1=K\cdot i#.

De formule #\sum_{j=1}^na_j =K# is een gevolg van de formules die er boven staan:

\[\begin{array}{rcl} \displaystyle\sum_{j=1}^na_j &=&(R_0-R_1)+(R_1-R_2)+\cdots (R_{n-1}-R_n)\\ &=&R_0-(R_1-R_1)-(R_2-R_2))-\cdots- (R_{n-1}-R_{n-1})-R_n\\ &=&R_0-R_n\\ &=&K-0\\ &=&K\end{array}\]

De formules geven aan dat, bij gegeven groeivoet #i#, beginkapitaal #K# en looptijd #n# van de lening alle schuldresten #R_j# en renteaflossingen #r_j# bekend zijn, zodra de aflossingen #a_j# bekend zijn. De verschillende typen leningen hangen daarvan af. We gaan nader in op drie soorten leningen:

Bulletlening: geen aflossing in tussentijdse periodes
Lineaire lening: constante aflossing per periode
Annuïteitenlening: constant totaal van aflossing en rente per periode

We zullen elk van deze leningen afzonderlijk bespreken. Hier gaan we in op de eerste, meest eenvoudige vorm.

Bulletlening

Een bulletlening is een lening waarbij er geen tussentijdse aflossingen plaatsvinden. De interest van #p\%# (ofwel groeivoet #i=\frac{p}{100}#) wordt aan het einde van elke tijdeenheid betaald. Het volledige geleende bedrag (#K#) wordt aan het einde van de looptijd (#n#) in één keer terugbetaald.

Een bulletlening wordt dus gekenmerkt door de volgende formules:

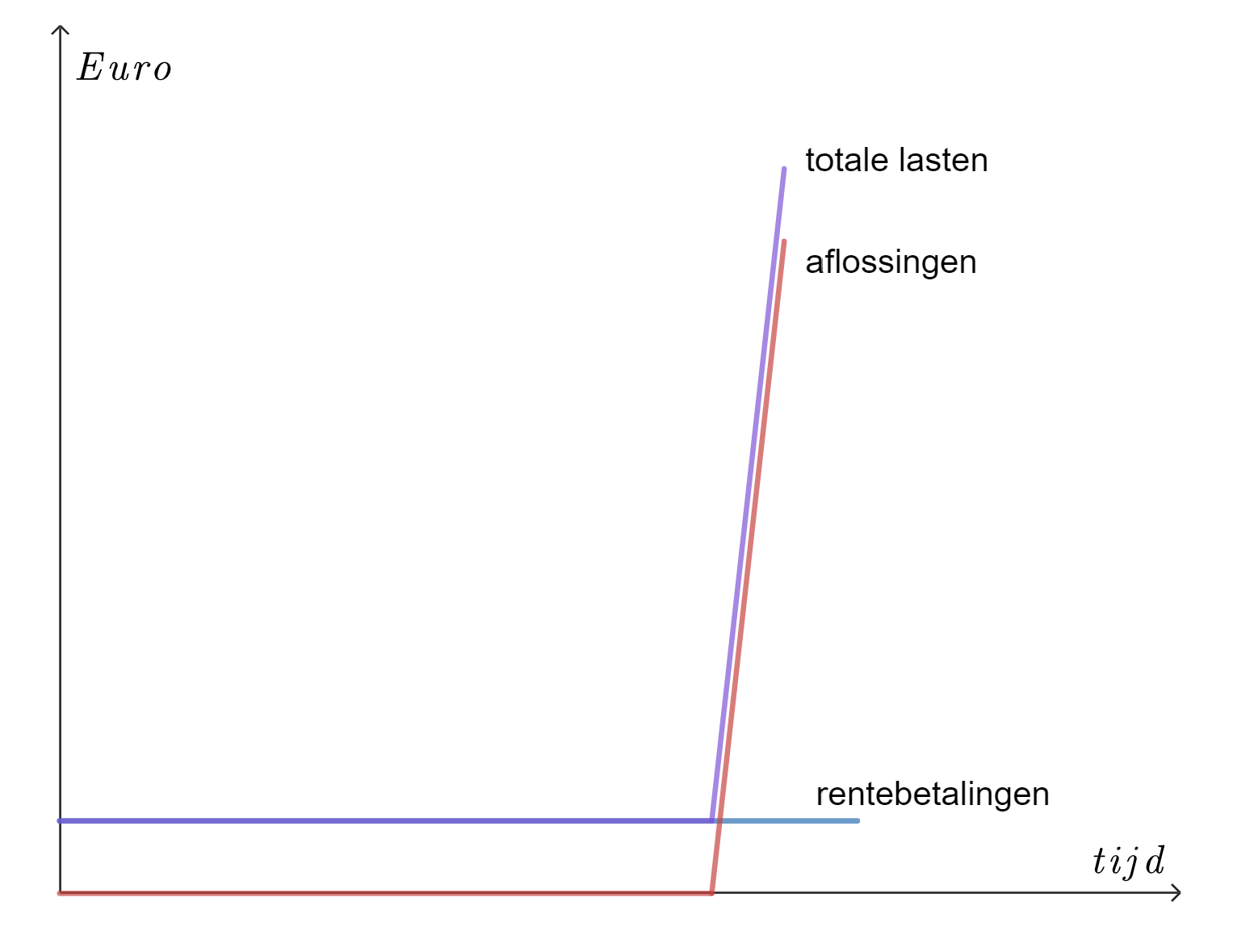
\[\begin{array}{rcl}\text{Aflossingen}&&a_1 = a_2 = a_3 =\cdots = a_{n-1} = 0\\ &&a_n = K\\ \text{Rentebetalingen}&& r_1 = r_2 = r_3 =\cdots = r_n = K\cdot i\\ \text{Schuldrest}&&R_1 = R_2 = R_3 =\cdots = R_{n-1} = K\\ &&R_n = 0\end{array}\]

Omdat er niet tussentijds wordt afgelost, moet gedurende de gehele looptijd van de lening rente betaald worden over het volledige geleende bedrag.

Dit type lening kenmerkt zich door relatief lage lasten gedurende de looptijd en een zeer hoge last wanneer de lening afloopt.

Een 10%-bulletlening van €100,000 met een looptijd van 10 jaar leidt tot onderstaande aflossingstabel.

Periode	Schuld begin	Rentebetaling	Aflossing	Schuld eind
#j#	#R_{j-1}#	#r_j#	#a_j#	#R_j#
1	100,000	10,000	0	100,000
2	100,000	10,000	0	100,000
3	100,000	10,000	0	100,000
4	100,000	10,000	0	100,000
5	100,000	10,000	0	100,000
6	100,000	10,000	0	100,000
7	100,000	10,000	0	100,000
8	100,000	10,000	0	100,000
9	100,000	10,000	0	100,000
10	100,000	10,000	100,000	0

In grafiek:

De rentebetaling voldoet bij elke lening die we bespreken aan #r_j = R_{j-1}\cdot i#. In dit geval geldt #R_{j-1}=K# voor elke #j#, dus #r_j=K\cdot i#.

Voorbeelden

Gegeven is een 10%-bulletlening van #\euro\,##30000# met een looptijd van #14# jaar.

Bereken de rentebetaling in jaar #3#.

#r_{3} =# #3000#

Gegeven:

kapitaal: #K = 30000#
interest: #i = 0.10#
looptijd: #n = 14#
periode: #j = 3#

Aangezien er bij een bulletlening geen tussentijdse aflossingen plaatsvinden, zal er elke periode rente betaald moeten worden over het volledige geleende bedrag. Dit bedrag wordt als volgt berekend:
\[\begin{array}{rcl}
r_j &=& K\cdot i\\\
&&\phantom{xxxxx}\color{blue}{\text{formule rentebetaling bulletlening in periode }j}\\
r_{3} &=& 30000\cdot 0.10\\
&&\phantom{xxxxx}\color{blue}{\text{waarden voor }j,\ K\text{ en }i\text{ ingevuld}}\\
&=& 3000\\
&&\phantom{xxxxx}\color{blue}{\text{uitgerekend}}\\
\end{array}\]

Nieuw voorbeeld