Het definiërende kenmerk van een annuïteitenlening is dat de totale lasten per periode constant blijven. Dit houdt in dat de hoogte van de rentebetaling en de aflossing dusdanig gekozen worden dat de som van deze betalingen elke periode hetzelfde bedrag oplevert. Dit bedrag noemt men de annuïteit, en wordt aangegeven met #Ann#.
De annuïteit voldoet aan:
\[\begin{array}{rcl}Ann &=& \dfrac{K\cdot i}{1-(1+i)^{-n}}\\&=& r_j +a_j\\\end{array}\]
Een annuïteitenlening wordt dus gekenmerkt door de volgende formules:
\[\begin{array}{rcl}\text{Aflossingen}&&a_1 =\dfrac{K\cdot i}{(1+i)^n-1} \\ &&a_j = a_1\cdot (1+i)^{j-1}\\ &&\sum_{}a_j = K \\ \text{Rentebetalingen}&&r_j = Ann - a_j\\ \text{Schuldrest}&&R_j = K\cdot \dfrac{1-(1+i)^{j-n}}{1-(1+i)^{-n}}\\ \end{array}\]
Net als bij een lineaire lening wordt er aan het einde van elke periode een deel van de schuld afgelost, met als gevolg dat de rentebetaling elke opeenvolgende periode daalt. Aan het begin van de looptijd wordt er relatief weinig afgelost, maar dit bedrag loopt op naarmate de tijd vordert.
#a_1 \lt a_2 \lt a_3 \lt \cdots \lt a_n#
#r_1 \gt r_2 \gt r_3 \gt \cdots \gt r_n#
Een 10%-annuïteitenlening van €100,000 met een looptijd van 10 jaar leidt tot onderstaande aflossingstabel.
| Periode |
Schuld begin |
Annuïteit |
Rentebetaling |
Aflossing |
Schuld eind |
| #j# |
#R_{j-1}# |
#Ann# |
#r_j# |
#a_j# |
#R_j# |
| 1 |
100,000.00 |
16,274.54 |
10,000.00 |
6,274.54 |
93,725.46 |
| 2 |
93,725.46 |
16,274.54 |
9,372.55 |
6,901.99 |
86,823.47 |
| 3 |
86,823.47 |
16,274.54 |
8,682.35 |
7,592.19 |
79,231.27 |
| 4 |
79,231.27 |
16,274.54 |
7,923.13 |
8,351.41 |
70,879.86 |
| 5 |
70,879.86 |
16,274.54 |
7,087.99 |
9,186.55 |
61,693.31 |
| 6 |
61,693.31 |
16,274.54 |
6,169.33 |
10,105.21 |
51,588.10 |
| 7 |
51,588.10 |
16,274.54 |
5,158.81 |
11,115.73 |
40,472.37 |
| 8 |
40,472.37 |
16,274.54 |
4,047.24 |
12,227.30 |
28,245.07 |
| 9 |
28,245.07 |
16,274.54 |
2,824.51 |
13,450.03 |
14,795.04 |
| 10 |
14,795.04 |
16,274.54 |
1,479.50 |
14,795.04 |
0 |
In grafiek:
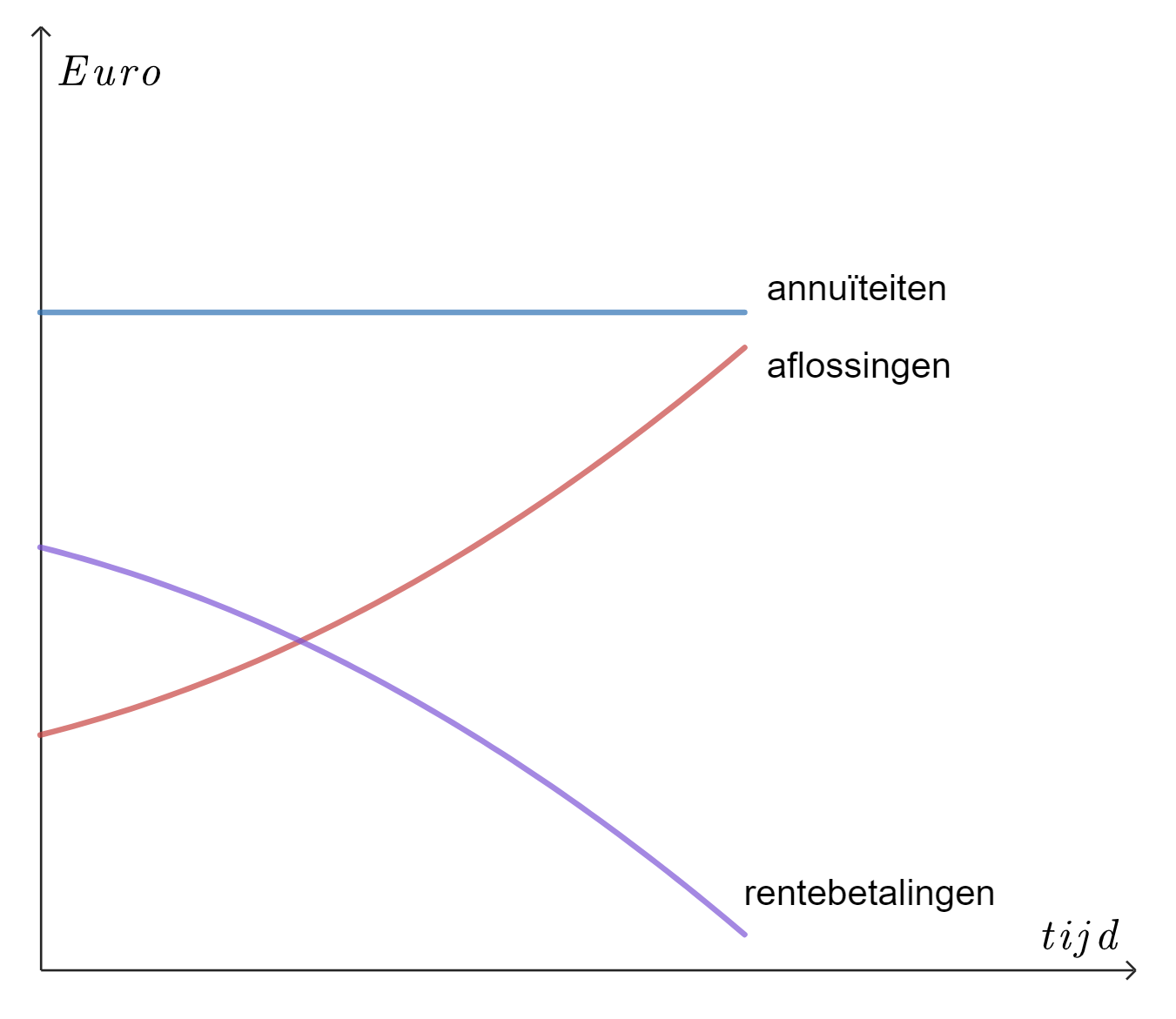
We gaan uit van het gegeven dat elke termijn een vast bedrag betaald wordt. Dit bedrag is #a_j+r_j# voor periode #j#. We laten eerst zien dat de aflossingen #a_j# van een annuïteitenlening in de periodes #j=1,2,\ldots# een meetkundige reeks vormen met reden #(1+i)#:
\[\begin{array}{lclcc}
&&Ann = r_j + a_j = r_{j+1} + a_{j+1} &(1)&\\
&&\phantom{xxxxxxx}\color{blue}{\text{kenmerkende formule annuïteit}}\\
&&r_j = i \cdot R_{j-1} &(2)&\\
&&\phantom{xxxxxxx}\color{blue}{\text{formule rentebetaling periode } j}\\
&&r_{j+1} = i \cdot R_j = i \cdot (R_{j-1} - a_j) = i\cdot R_{j-1} - i\cdot a_j &(3)&\\
&&\phantom{xxxxxxx}\color{blue}{\text{formule rentebetaling periode }j + 1}&&\\
&&i\cdot R_{j-1} + a_j = i\cdot R_{j-1} - i\cdot a_j + a_{j+1}&&\\
&&\phantom{xxxxxxx}\color{blue}{\text{(2) en (3) ingevuld in tweede gelijkheid van (1)}}&&\\
&&a_{j+1}=a_j+i\cdot a_j\\
&&\phantom{xxxxxxx}\color{blue}{\text{de vorige vergelijking vereenvoudigd}}&&\\
&& a_{j+1}=a_j\cdot (1+i)&& \\
&&\phantom{xxxxxxx}\color{blue}{a_j\,\,\text{buiten haakjes gehaald}}&&\\
\end{array}\]
Dit laat zien dat inderdaad #a_j=a_1\cdot (1+i)^{j-1}#. Om #a_1# te bepalen, gebruiken we het feit dat de som van alle aflossingen gelijk is aan het beginkapitaal #K#:
\[\begin{array}{rcl}K&=&\sum_{j=1}^na_j \\ &=&a_1\cdot\sum_{j=1}^n{(1+i)^{j-1}} \\ &&\phantom{xx}\color{blue}{a_j = a_1\cdot (1+i)^{j-1}}\\ &=&a_1\cdot\dfrac{(1+i)^{n}-1}{1+i-1} \\ &&\phantom{xx}\color{blue}{\text{meetkundige reeks}}\\ &=&a_1\cdot\dfrac{(1+i)^{n}-1}{i}\end{array}\]
We vinden dus de lineaire vergelijking #a_1\cdot\dfrac{(1+i)^{n}-1}{i}=K# met onbekende #a_1#, waaruit volgt
\[a_1 = \dfrac{K\cdot i}{(1+i)^n-1}\]
Nu we alle #a_j# kennen, berekenen we de restschulden #R_j# als volgt:
\[\begin{array}{rcl}
R_j &=& R_{j-1}-a_j = R_{j-2}-a_{j-1}-a_j=\cdots\\ &=&R_0-a_1-a_2-\cdots-a_j\\ &=&K-a_1\cdot\left(1+(1+i)+(1+i)^2+\cdots+(1+i)^{j-1}\right)\\ &=&K-a_1\cdot \dfrac{(1+i)^j-1}{i}\\ &&\phantom{xxxxxxx}\color{blue}{\text{meetkundige reeks}}\\&=&K- \dfrac{K\cdot i}{(1+i)^n-1}\cdot \dfrac{(1+i)^j-1}{i}\\ &&\phantom{xxxxxxx}\color{blue}{\text{formule voor }a_1\text{ ingevuld}}\\&=&K- \dfrac{K\cdot \left((1+i)^j-1\right)}{(1+i)^n-1}\\&&\phantom{xxxxxxx}\color{blue}{\text{breuken vermenigvuldigd}}\\ &=&K\cdot\dfrac{(1+i)^n-1- \left((1+i)^j-1\right)}{(1+i)^n-1}\\&&\phantom{xxxxxxx}\color{blue}{\text{alles rechts onder één noemer gebracht}} \\&=& K\cdot \dfrac{1-(1+i)^{j-n}}{1-(1+i)^{-n}}\\
&&\phantom{xxxxxxx}\color{blue}{\text{breuk vereenvoudigd}}
\end{array}\]
De rentebetalingen #r_j# zijn direct gerelateerd aan de restschulden:
\[
r_j = i\cdot R_{j-1}= i\cdot K\cdot \dfrac{1-(1+i)^{j-1-n}}{1-(1+i)^{-n}}
\]
We concluderen dat inderdaad #Ann=a_j+r_j# constant (dat wil zeggen: niet van #j# afhangt) is voor de gevonden waarden van #a_j# en #r_j#:
\[\begin{array}{rcl}
a_j+r_j &=&a_1\cdot (1+i)^{j-1}+i\cdot K\cdot \dfrac{1-(1+i)^{j-1-n}}{1-(1+i)^{-n}}\\&&\phantom{xxxxxxx}\color{blue}{\text{formules voor }a_j\text{ en }r_j\text{ ingevuld}} \\ &=& \dfrac{K\cdot i}{(1+i)^n-1}\cdot (1+i)^{j-1}+i\cdot K\cdot \dfrac{(1+i)^n-(1+i)^{j-1}}{(1+i)^{n}-1}\\ &&\phantom{xxxxxxx}\color{blue}{\text{formule voor }a_1\text{ ingevuld}}\\ &=& K\cdot i\cdot \dfrac{ (1+i)^{j-1}+ (1+i)^n-(1+i)^{j-1}}{(1+i)^{n}-1}\\ &&\phantom{xxxxxxx}\color{blue}{\text{gelijknamige breuken opgeteld}}\\ &=& K\cdot i\cdot \dfrac{ (1+i)^n}{(1+i)^{n}-1}\\&&\phantom{xxxxxxx}\color{blue}{\text{termen met }j\text{ tegen elkaar weggestreept}}\\ &=&\dfrac{K\cdot i}{1-(1+i)^{-n}}\\&&\phantom{xxxxxxx}\color{blue}{\text{teller en noemer gedeeld door }(1+i)^n} \end{array}\]
De laatste uitdrukking is de formule voor #Ann# in de stelling.
De formule voor de annuïteit #Ann# is ook af te leiden door #Ann# op te vatten als contante waarde bij postnumerando rente met vaste termijnen:
\[\begin{array}{rcl}
a_{\left .n\right \rceil i} &=& \dfrac{1-(1+i)^{-n}}{i}\\
&&\phantom{xxxxxxx}\color{blue}{\text{formule contante waarde factor}}\\
Ann &=& \dfrac{K}{a_{n|i}}\\
&&\phantom{xxxxxxx}\color{blue}{\text{formule annuïteit}}\\
&=& \dfrac{K}{\dfrac{1-(1+i)^{-n}}{i}}\\
&&\phantom{xxxxxxx}\color{blue}{a_{n|i}\,\,\text{ingevuld}}\\
&=& K \cdot \dfrac{i}{1-(1+i)^{-n}}\\
&&\phantom{xxxxxxx}\color{blue}{\text{delen door breuk is vermenigvuldigen met omgekeerde}}\\
&=& \dfrac{K\cdot i}{1-(1+i)^{-n}}\\
&&\phantom{xxxxxxx}\color{blue}{\text{vereenvoudigd}}\\
\end{array}\]
Herleiding van de formule voor het berekenen van de schuldrest:
\[\begin{array}{rcl}
R_j &=& Ann \cdot a_{n-j|i}\\
&&\phantom{xxxxxxx}\color{blue}{\text{formule schuldrest annuïteitenlening}}\\
&=&\dfrac{K\cdot i}{1-(1+i)^{-n}}\cdot \dfrac{1-(1+i)^{-(n-j)}}{i}\\
&&\phantom{xxxxxxx}\color{blue}{Ann\,\text{en }a_{n-j|i}\,\text{ingevuld}}\\
&=& K\cdot \dfrac{1-(1+i)^{j-n}}{1-(1+i)^{-n}}\\
&&\phantom{xxxxxxx}\color{blue}{\text{vereenvoudigd}}\\
\end{array}\]
Gegeven is een 3%-annuïteitenlening van #\euro\,##130000# met een looptijd van #8# jaar. Dit percentage betreft de jaarlijkse interest.
Bereken de annuïteit van deze lening bij maandelijkse betaling, afgerond op twee decimalen.
Maandelijkse annuïteit #=# #1522.46#
Gegeven:
- kapitaal: #K = 130000#
- groeivoet: #i =i_{\text{jaar}} = 0.03#
- looptijd: #n =n_{\text{jaar}} = 8#
Om de gevraagde annuïteit te berekenen, bepalen we eerst de interest per maand en de looptijd in maanden. Beide gebruiken het feit dat een jaar bestaat uit 12 maanden.
Volgens een omrekeningsformule voor groeivoeten, die volgt uit de
omrekeningsformule voor groeifactoren,
geldt voor de maandelijks rentevoet \[i_{\text{maand}} = \left(1+i_{\text{jaar}}\right)^{\frac{1}{12}} - 1\approx 0.00246627\]
Verder geldt voor de looptijd \[i_{\text{maand}} = 12\cdot 8 = 96 \]
De maandelijkse annuïteit wordt nu als volgt berekend:
\[\begin{array}{rcl}
Ann_{\text{maand}} &=& \dfrac{K\cdot i_{\text{maand}}}{1-(1+i_{\text{maand}})^{-n_{\text{maand}}}}\\
&&\phantom{xxxxx}\color{blue}{\text{de formule voor de annuïteit}}\\
&\approx & \dfrac{130000\cdot 0.00246627}{1-(1+0.00246627)^{-96}}\\
&&\phantom{xxxxx}\color{blue}{\text{waarden voor }K, i_{\text{maand}}\text{ en }n_{\text{maand}}\text{ ingevuld}}\\
&\approx& 1522.46\\
&&\phantom{xxxxx}\color{blue}{\text{uitgerekend}}\\
\end{array}\]
 Annuïteiten
Annuïteiten





