Optimalisatie: Economische toepassingen
 Verwacht rendement en vermogensstructuur
Verwacht rendement en vermogensstructuur
Ondernemingen streven naar het realiseren van een optimale vermogensstructuur. Dit is een combinatie van eigen en vreemd vermogen waarbij de gemiddelde kosten van het vermogen van het bedrijf zo laag mogelijk uitvallen. Over het algemeen geldt dat vreemd vermogen goedkoper is dan eigen vermogen. Dit heeft er onder andere mee te maken dat betaalde rente op het vreemd vermogen zowel bedrijfseconomisch als fiscaal als kosten gezien worden. Op het eerste gezicht lijkt het dus optimaal voor een ondermening om zoveel mogelijk vreemd vermogen aan te trekken.
Het aantrekken van grote hoeveelheden vreemd vermogen kent echter ook een keerzijde. Dit heeft te maken met de rol die het eigen vermogen binnen een onderneming vervult. Eén van de functies van het eigen vermogen is namelijk om als een buffer te dienen die schommelingen in de winst moet opvangen. Wanneer een onderneming grote hoeveelheden vreemd vermogen aantrekt wordt deze buffer relatief gezien steeds kleiner. Hierdoor neemt het risico voor de aandeelhouders en verschaffers van het vreemd vermogen toe. Ter compensatie van dit toegenomen risico zullen deze investeerders een hoger rendement gaan eisen, waardoor de kosten voor de onderneming zullen toenemen.
In de onderstaande grafiek is de verhouding tussen het vreemd en eigen vermogen uitgezet tegenover de kosten van het vermogen. Er bestaat voor een onderneming dus een optimale verhouding tussen het vreemd en eigen vermogen waarbij de kosten van het vermogen geminimaliseerd worden.
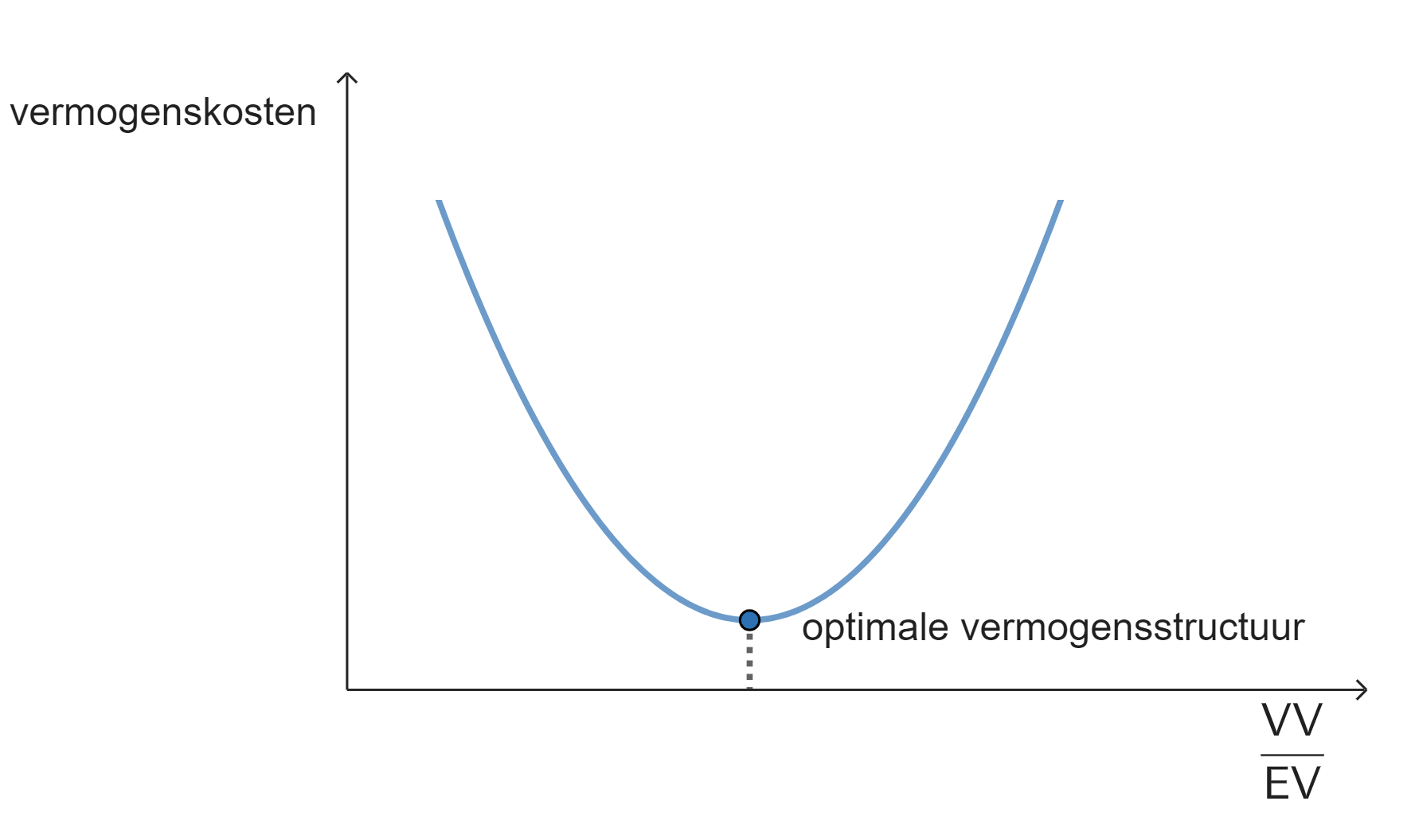
Financiële hefboomformule
De rendementeis van vermogensverschaffers hangt dus mede af van de verhouding tussen eigen en vreemd vermogen. We geven deze verhouding weer met behulp van de financiële hefboomformule:
\[REV = (1-b)(RTV + (RTV – Kvv) \cdot \dfrac{VV}{EV})\]
In de vergelijking hebben de symbolen de volgende betekenis:
\[\begin{array}{rcl}
b &=& \text{belastingtarief}\\
REV &=& \text{rentabiliteit van het eigen vermogen} = \dfrac{\text{nettowinst nb}}{\text{eigen vermogen}}\\
RTV &=& \text{rentabiliteit van het totaal vermogen} = \dfrac{\text{bedrijfsresultaat}}{\text{totaal vermogen}}\\
Kvv &=&\text{kostenvoet van het vreemd vermogen} = \text{risicovrije rente}+\text{renteopslag} \cdot \dfrac{VV}{EV}\\
VV &=&\text{marktwaarde van het vreemd vermogen}\\
EV &=&\text{marktwaarde van het eigen vermogen}\\
\dfrac{VV}{EV} &=& \text{financiële hefboomfactor}\\
\end{array}\]
Factoren
In de hefboomformule kunnen de volgende factoren onderscheiden worden:
1. De factor #(1-b)# bepaalt het percentage van de rente op vreemd vermogen dat door de onderneming zelf betaald wordt. De rente die een onderneming moet betalen als gevolg van openstaande schulden mag in de resultatenrekening als kosten verrekend worden. Dit levert de onderneming een belastingvoordeel op wat ook wel een belastingschild genoemd wordt.
2. De hefboomfactor #\dfrac{VV}{EV}#. De hefboomfactor geeft de verhouding weer tussen het vreemd en eigen vermogen en wordt ook wel leverage genoemd. Ondernemingen met een hoge leverage worden gekenmerkt door grote hoeveelheden vreemd vermogen en worden over het algemeen als risicovoller beschouwd.
3. De rentemarge #(RTV – Kvv)#. De rentemarge is een indicatie van het verschil tussen de rente op het vreemd vermogen enerzijds en het rendement van de onderneming anderzijds. Wanneer het rendement op vreemd vermogen toeneemt, zal de rentemarge afnemen.
4. De factor #(RTV - Kvv) \cdot \dfrac{VV}{EV}# noemen we het hefboomeffect.
- belastingtarief: #b = 40\%#
- rentabiliteit van het totale vermogen: #RTV = 10\%#
- risico-vrij rentepercentage #= 3\%#
- opslagpercentage #= 2\%#
Om de waarde voor van de hefboomfactor #{\dfrac{VV}{EV}}^*# te vinden waarvoor de rentabiliteit van het eigen vermogen #REV# gemaximaliseerd wordt voeren we de volgende handelingen uit:
\[\begin{array}{rcl}
REV &=& (1-b) \left(RTV + (RTV - Kvv) \cdot \dfrac{VV}{EV}\right)\\
&&\phantom{xxxxx}\color{blue}{\text{formule rentabiliteit eigen vermogen}}\\
&=& (1-b) \left(RTV + (RTV - (\text{risicovrije rente} + \text{renteopslag} \cdot \dfrac{VV}{EV} )) \cdot \dfrac{VV}{EV}\right)\\
&&\phantom{xxxxx}\color{blue}{\text{formule voor }Kvv \text{ ingevuld}}\\
&=& (1-b) \left(RTV + (RTV - (\text{risicovrije rente} + \text{renteopslag} \cdot x )\right) \cdot x)\\
&&\phantom{xxxxx}\color{blue}{\dfrac{VV}{EV}\text{ gelijkgesteld aan } x}\\
&=& (1-0.40) (0.100 + (0.100 - (0.030 + 0.020 \cdot x)) \,x)\\
&&\phantom{xxxxx}\color{blue}{\text{waarden voor }b, RTV, \text{risicovrije rente en opslagpercentage ingevuld}}\\
&=& 0.6 \cdot (0.100 + (0.100 x - 0.030 x - 0.020 x^2)\\
&&\phantom{xxxxx}\color{blue}{\text{tussenstap uitwerking haakjes}}\\
&=& 0.06 + 0.06 x - 0.018x -0.012 x^2\\
&&\phantom{xxxxx}\color{blue}{\text{haakjes uitgewerkt}}\\
&=& -0.012 x^2 + 0.042x + 0.06\\
&&\phantom{xxxxx}\color{blue}{\text{versimpeld en volgorde herschreven}}\\
\end{array}\]
We hebben nu een formule voor de rentabiliteit van het eigen vermogen in de vorm #ax^2 + bx + c# met:
- #a = -0.012#
- #b = 0.042#
- #c = 0.060#
\[\begin{array}{rcl}
x_{top} &=& -\dfrac{b}{2 a}\\
&&\phantom{xxxxx}\color{blue}{\text{formule }x_{top} \text{ voor kwadratische functie}}\\
&=& -\dfrac{0.042}{2\cdot-0.012}\\
&&\phantom{xxxxx}\color{blue}{\text{waarden voor }a \text{ en }b \text{ ingevuld}}\\
&\approx& 1.75\\
&&\phantom{xxxxx}\color{blue}{\text{uitgerekend}}\\
&\approx& {\dfrac{VV}{EV}}^*\\
\end{array}\]

omptest.org als je een OMPT examen moet maken.



