[A, SfS] Chapter 3: Probability Distributions: 3.2: The Normal Distribution
 The Normal Distribution
The Normal Distribution
The Normal Distribution
In this lesson, you will learn about the normal distribution. Many continuous random variables that model natural and social phenomena follow the normal distribution. This is the most important distribution in the field of statistics.
#\text{}#
Normal Probability Distribution
A continuous random variable #X# is normally distributed around its mean #\mu# with variance #\sigma^2 > 0# (and standard deviation #\sigma#) if it's probability density function (pdf) is:
\[f(x) = \frac{1}{\sigma\sqrt{2\pi}}e^{-\frac{(x - \mu)^2}{2\sigma^2}}\]
for all #x# in #(-\infty,\infty)#.
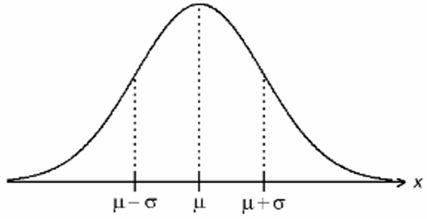
In this case we write #X \sim N\big(\mu,\sigma^2\big)#.
The graph of the density curve corresponding to #f(x)# is shown in the figure at the right. The peak of the curve occurs when #x = \mu#. This curve is often called the “bell curve”, for obvious reasons. The width of the “bell” is determined by the size of #\sigma#. On either side of the curve you can see the inflection points where the concavity of the curve changes (where #f’’(x) = 0#). These inflection points are at #x = \mu \pm \sigma#. Because the area below the curve must equal one, the peak of the curve must be higher when #\sigma# is small, and must be lower when #\sigma# is large.
Note that, although in the figure it appears that the curve touches the #x# axis, in fact the curve never reaches the #x# axis, but only approaches the axis as a horizontal asymptote. We often called the left and right sides of the density curve the “left and right tails”.
#\text{}#
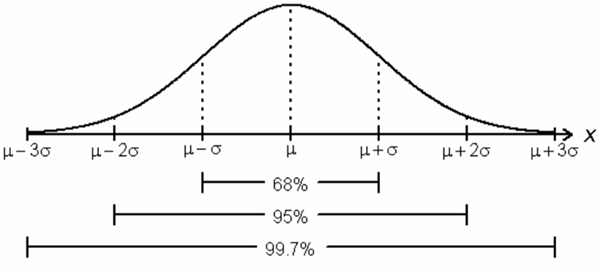
Empirical Rule
If #X \sim N\big(\mu,\sigma^2\big)#, then there is an approximate probability of #0.68# that an observed measurement of #X# will fall into the interval #(\mu - \sigma, \mu + \sigma)#.
Furthermore, there is an approximate probability of #0.95# that an observed measurement of #X# will fall into the interval #(\mu - 2\sigma, \mu + 2\sigma)#.
Lastly, there is an approximate probability of #0.997# that an observed measurement of #X# will fall into the interval #(\mu - 3\sigma,\mu + 3\sigma)#.
Hence it would be very unusual to observe a value of #X# that is more than #3# standard deviations away from the mean.
#\text{}#
The distribution of a continuous non-random variable on a population can also be described as Normal, with mean #\mu# and variance #\sigma^2#.
Normal Distribution and Sampling
If a random sample is selected from a population for which some non-random variable has a normal distribution, then the distribution of the same variable on the sample itself should also be approximately normal (i.e., a histogram of the variable measured on the sample would have a similar shape to the density curve shown above).
Moreover, if a non-random variable has a #N\big(\mu,\sigma^2\big)# distribution on a population, and we plan to randomly select a member of the population and measure that variable, and we let #X# denote the outcome of that measurement, then #X# is a random variable which has a #N\big(\mu,\sigma^2\big)# probability distribution.
Height in cm of adult men in the Netherlands is normally distributed with mean #183#cm and standard deviation #10#cm.
Thus around #68\%# of Dutch men are between #173#cm and #193#cm tall, around #95\%# of Dutch men are between #163#cm and #203#cm, and nearly #100\%# are between #153#cm and #213#cm.
Furthermore, if #X# is the height of a randomly-selected Dutch man, then #X \sim N\big(183,10^2\big)#.
#\text{}#
Approximating the Normal Distribution
Sometimes a variable is not continuous, but its range consists of many possible values, and the histogram of its frequency distribution over the values has the shape of the density curve of the normal distribution.
It is then often convenient to approximate the distribution of such a variable with the normal distribution.
An example of such a variable is IQ (Intelligence Quotient), a measure developed by psychologists to assess human intelligence.
The IQ score is always a positive integer, generally between #50# and #150#, and the shape of the histogram of its frequency distribution has the shape of a normal density curve. Since it must be an integer, it is not continuous, but its range covers #100# values or so.
So psychologists consider the IQ scores of the human population to be approximately normally distributed with a mean of #100# and a standard deviation of #15#. Therefore about #95\%# of the human population has IQ scores between #70# and #130#. Those with IQ scores above #130# are considered exceptionally intelligent, while those with IQ scores close to #100# are considered to have average intelligence. Those with IQ scores below #70# generally have difficulty functioning independently in society.
If we plan to select a person randomly from a human population and measure the person's intelligence using the IQ test, and we let #X# denote the future outcome of that measurement, then we can regard #X# as a normally-distributed random variable with mean #100# and standard deviation #15#.
#\text{}#
A special case of the normal distribution is the standard normal distribution.
Standard Normal Distribution
The standard normal distribution is a normal distribution with a mean of #0# and a standard deviation of #1#.
We usually use the letter #Z# to denote a random variable that has a standard normal distribution, and write #Z \sim N\big(0,1\big)#.
Standardizing
An important and useful fact that you will need to remember is: If
\[X \sim N \big( \mu, \sigma^2 \big) \]
and we define
\[Z = \frac{X - \mu}{\sigma}\]
then
\[Z \sim N \big( 0, 1 \big) \]
The conversion of #X# to #Z# shown here is called standardizing, and the result is often referred to as the Z-score.
An observed value of a normally-distributed random variable #X# has a #Z#-score of #-1.84#.
If the mean of #X# is #63# and the variance of #X# is #25#, what was the original score?
\[\begin{array}{rcl}
Z &=&\cfrac{X - \mu}{\sigma}\\
-1.848 &=& \cfrac{X - 63}{5}
\end{array}\]
Solving this for #X# gives us #X = 53.76#.
Before statistical software became widely available, standardizing was necessary in order to compute probabilities using a table of standard normal distributions found in the appendices of most statistics books. While this is not needed anymore, we still use standardizing in other contexts, such as to compare two different normally-distributed random variables.
#\text{}#
Suppose it is given that #X \sim N\big(\mu,\sigma^2\big)#. Since #X# is continuous, #\mathbb{P}(X = x) = 0# for every real number #x#. We can only compute probabilities for #X# to fall into an interval of real numbers.
In practice, as noted earlier, there are many cases where the random variable is not actually continuous but we are approximating its distribution with the normal distribution, as with the IQ scores.
Since an IQ score is usually one of the values in the set #\{50,51,...,149,150\}# (excluding super-geniuses), the probability of observing #X = x# for any #x# in this set could not be zero. We can handle this properly by using a continuity correction.
Continuity Correction
In probability theory, a continuity correction is an adjustment that is made when a discrete distribution is approximated by a continuous distribution.
If we really want #\mathbb{P}(X = 120)# we would actually have to find #\mathbb{P}(119.5 \leq X \leq 120.5)#.
Similarly, if we really want #\mathbb{P}(X \geq 113)# we should actually compute #\mathbb{P}(X \geq 112.5)#, and if we want #\mathbb{P}(X \leq 87)# we should use #\mathbb{P}(X \leq 87.5)#.
That is, we should go halfway above and/or below the values to account for the fact that we are treating the integers as if they are continuous.
#\text{}#
Normal Probability Calculations
To compute the probability for a normally-distributed random variable #X# to be observed in some interval, we would have to compute an integral of its pdf over the interval.
That is, if #X \sim N\big(\mu,\sigma^2\big)#, then:
\[\begin{array}{rcl}
\mathbb{P}(X \leq x) &=& \displaystyle\int_{-\infty}^{x}\frac{1}{\sigma\sqrt{2\pi}}e^{-\frac{(t-\mu)^2}{2\sigma^2}}dt\\\\
\mathbb{P}(X \geq x) &=& \displaystyle\int_{x}^{\infty}\frac{1}{\sigma\sqrt{2\pi}}e^{-\frac{(t-\mu)^2}{2\sigma^2}}dt\\\\
\mathbb{P}(x_1 \leq X \leq x_2) &=& \displaystyle\int_{x_1}^{x_2}\frac{1}{\sigma\sqrt{2\pi}}e^{-\frac{(t-\mu)^2}{2\sigma^2}}dt
\end{array}\]
Before you begin to panic about having to carry out the computation of integrals of these forms, you should know that there is no way to do so analytically. These computations have to be done using numerical methods, which are programmed into statistical software. Before such software was widely available, one had to first standardize, then use tables in a statistics book. But we will use #\mathrm{R}# in this course.
#\text{}#
Quantiles of the Normal Distribution
Suppose #X \sim N\big(\mu,\sigma^2\big)#. We might also want the #p#th quantile #x_p# of #X# that satisfies
\[F(x_p) = \mathbb{P}(X \leq x_p) = p\]
for any #p# in #(0,1)#.
This means that the area beneath the normal density curve to the left of #x_p# equals #p#, i.e.,
\[p = \int_{-\infty}^{x_p}\frac{1}{\sigma\sqrt{2\pi}}e^{-\frac{(t-\mu)^2}{2\sigma^2}}dt\]
In statistics we will be most interested in quantiles of the standard normal distribution. When we use the standard normal distribution, we use #z# in place of #x#. So, for #Z \sim N\big(0,1\big)#, the #p#th quantile of #Z# is represented by #z_p#.
Because the standard normal distribution is symmetric around #0#, we have the property that #z_p = -z_{1-p}# for every #p# in #(0,1)#.
For example, #z_{0.05} \approx -1.645# and #z_{0.95} \approx 1.645#, while #z_{0.975} \approx 1.96# and #z_{0.025} \approx -1.96#.
This means that
\[\mathbb{P}(-1.645 \leq Z \leq 1.645) \approx 0.90\]
and
\[\mathbb{P}(-1.96 \leq Z \leq 1.96) \approx 0.95\]
In general, for any specified #p#, the computation of #z_p# cannot be done analytically, but is found using statistical software or tables in statistics books. But the two pairs of quantiles given above occur frequently enough in statistics that you might want to eventually memorize them.
#\text{}#
Linear Combinations of a Single Normally-Distributed Variable
If #X\sim N\big(\mu, \sigma^2\big)# and #a# and #b# are any constants from the real numbers with #a \neq 0# and we define
\[Y= aX +b\]
then
\[Y\sim N\big(a\mu+b, a^2\sigma^2\big)\]
So for example, if #X# is the IQ score (recall #X\sim N\big(100, 15^2\big)#), and we define
\[Y=0.5X - 20\]
then
\[Y \sim N\big((0.5)(100) - 20, (0.5)^2(15)^2\big) = N\big(30, 56.25\big)\]
#\text{}#
Linear Combinations of Two Normally-Distributed Variables
Now suppose we have two random variables, #X# and #Y#, with #X \sim N\big(\mu_1, \sigma^2_1)# and #Y \sim N\big(\mu_2, \sigma^2_2)#, and suppose #X# and #Y# are independent. Then
\[X+Y \sim N\big(\mu_1 + \mu_2,\,\, \sigma^2_1 + \sigma^2_2\big) \]
and
\[X - Y \sim N\big(\mu_1 - \mu_2,\,\, \sigma^2_1 + \sigma^2_2\big) \]
Note carefully that the variances are added even when we have #X-Y#. This is because, for any real constants #a# and #b#:
\[aX + bY \sim N\big(a\mu_1 + b\mu_2, a^2\sigma^2_1 + b^2\sigma^2_2\big)\]
We would think of #X-Y# as #(1)X + (-1)Y#.
#\text{}#
Linear Combinations of n Normally-Distributed Variables
Finally, suppose we have #n# random variables #X_1, X_2, \ldots, X_n#, each of which has the #N\big( \mu,\sigma^2\big) # distribution, i.e.:
\[X_i \sim N\big(\mu, \sigma^2\big)\]
for #i = 1, 2, \ldots, n#.
Suppose further that these #n# random variables are mutually independent. Then the following results hold:
\[\begin{array}{rcccl}
\text{if}& S = \displaystyle\sum_{i=1}^n X_i &\text{then} & S \sim N\big(n\mu, n\sigma^2\big)
\end{array}\]
and
\[\begin{array}{rcccl}
\text{if}& \bar{X} = \cfrac{S}{n} &\text{then} & \bar{X} \sim N\Big(\mu, \cfrac{\sigma^2}{n}\Big)
\end{array}\]
#\text{}#
Sampling from a Normally-Distributed Population
This means that, if some continuous non-random variable has a #N \sim \big(\mu, \sigma^2 \big)# distribution on a population, and we plan to select a random sample of size #n# from that population and measure that variable on the elements of the sample, and we denote those future measurements by #X_1, X_2, \ldots , X_n#, then:
\[X_i \sim N \big(\mu, \sigma^2 \big)\]
Furthermore, the mean of those measurements on the sample (i.e. the sample mean) is also a normally-distributed random variable with parameters:
\[\bar{X} \sim N \big(\mu, \cfrac{\sigma^2}{n} \big)\]
As you can see the sample mean has a smaller standard deviation than the individual measurements, and its standard deviation gets smaller as the size of the sample gets larger.
This implies that when the sample size is large, the probability that the sample mean is close in value to the true mean is very high. That will be very useful in statistics when we don't actually know the true value of the mean.
#\text{}#
Using R
Normal Probability Calculations
If #X \sim N\big(\mu,\sigma^2\big)# and you want #\mathbb{P}(X \leq x)#, you can compute this in #\mathrm{R}# using the function #\mathtt{pnorm()}#:
> pnorm(x,μ,σ)
Note very carefully that you must use the standard deviation in the #\mathrm{R}# command, not the variance.
In particular, if #Z \sim N\big(0,1\big)# and you want #\mathbb{P}(Z \leq z)#, you can compute this is #\mathrm{R}# using
> pnorm(z)
In other words, if you are working with the standard normal distribution, you don't need to specify the value of the mean or the standard deviation. The #\mathrm{R}# command assumes you are working with the standard normal distribution unless you specify some other values for the mean and standard deviation.
Normal Probability of the Complement
If you want the complement probability, i.e., #\mathbb{P}(X \geq x)# or #\mathbb{P}(Z \geq z)#, you could subtract the above probabilities from #1#.
But you can also use an extra setting in the original #\mathrm{R}# commands given above:
> pnorm(x,μ,σ,low=F)
> pnorm(z,low=F)
The setting #\mathtt{low=F}# gives the area to the right of #x# (or #z#) under the density curve rather than the area to the left.
Calculating Normal Quantiles
If instead you know the probability #p# and you need the quantile #x_p# (or #z_p# for the standard normal), in #\mathrm{R}# you use the function #\mathtt{qnorm()}#:
> qnorm(q,μ,σ)
Or, if you have a standard normal distribution, use:
> qnorm(p)
If you want #p# to be the area to the right of the quantile rather than the area to its left, you can add the setting #\mathtt{low=F}# as above. Or else just replace #p# with #1 - p#.
So
> qnorm(0.975)
would give the same value as
> qnorm(0.025,low=F)
Generating a Random Sample from a Normal Distribution
You might want to generate a random sample of size #n# from a #N\big(\mu,\sigma^2\big)# distribution. This is done in #\mathrm{R}# using the function #\mathtt{rnorm()}#:
> rnorm(n,μ,σ)
Or, if you have a standard normal distribution, use:
> rnorm(n)
You may recall that for the binomial distribution there was an #\mathrm{R}# function #\mathtt{dbinom()}# that gives you the probability that #X = x#. There is also an #\mathrm{R}# function #\mathtt{dnorm()}#, but this does not give you the probability that #X = x#, which we know is #0# for a continuous random variable.
Instead, it gives you the value of the normal pdf #f(x)# at any real number #x#. This is useful if you want to make a plot of the normal density curve. But in this statistics course we will not need this function.
The weight in grams of an advertised #35#-gram package of a food product is normally distributed with a mean of #35# grams and a standard deviation of #0.017# grams.
A package is randomly selected from the shelf of a supermarket and its weight is precisely measured. What is the probability that its weight differs from #35# grams by more than #0.02# grams?
The weight differs from #35# grams by more than #0.02# grams if the weight is below #34.98# or above #35.02#. So if we denote the weight by #W#, we need #\mathbb{P}(W \leq 34.98) + \mathbb{P}(W \geq 35.02)#.
Since #W \sim N \big(35, 0.017^2 \big)#, we use in #\mathrm{R}#:
> pnorm(34.98, 35, 0.017) + pnorm(35.02, 35, 0.017, low=F)
[1] 0.2394
Due to the symmetry around the mean, these two probabilities are equal, so it also suffices to use:
> 2*pnorm(34.98, 35, 0.017)
[1] 0.2394

Or visit omptest.org if jou are taking an OMPT exam.



