[A, SfS] Chapter 8: Correlation and Regression: 8.1: Correlation
 Correlation
Correlation
CorrelationIn this section, we will discuss to how to assess the strength and direction of the linear association between two quantitative variables.
#\text{}#
Linear CorrelationConsider two quantitative random variables measured on a population.
If one of the variables has a tendency to change (either increasing or decreasing) by some fixed amount whenever the other variable increases by one unit, we say that the two variables are linearly correlated, and assign a measure for that linear correlation between #-1# and #1#, inclusive.
This measure is generally referred to as the population correlation coefficent and is denoted #\rho#.
Note that by “tendency” here we refer to the average behavior over the entire population, while accepting that the variables do not behave the same way for all individual members of the population.
If #\rho > 0#, then the tendency is for one of the variables to increase whenever the other one increases, i.e., a positive association.
When #|\rho|# is close to #1#, this tendency is very strong, and as #|\rho|# decreases, the tendency grows weaker.
If #\rho = 0#, then there is no tendency at all, i.e., the variables are uncorrelated.
It should be emphasized that we are only discussing linear association here. It could be that the two variables have a very strong non-linear association, in which case the use of #\rho# to describe their association would not make any sense.
\[\text{}\]
Pearson Sample Correlation CoefficientConsider a random sample of size #n# from the population, with measurements on two quantitative variables #X# and #Y# for each element in the sample. This gives us a set of bivariate data #(x_1,y_1),...,(x_n,y_n)#.
The Pearson sample correlation coefficient #r# can then be computed as the average of the products of the standardized measurements over the sample:
\[\begin{array}{rcl}
r &=& \cfrac{1}{n - 1} \displaystyle\sum_{i=1}^n \bigg(\cfrac{x_i - \bar{x}}{s_x}\bigg)\bigg(\cfrac{y_i - \bar{y}}{s_y}\bigg) \\\\
&=& \cfrac{\displaystyle\sum_{i=1}^n \Big(x_i - \bar{x} \Big)\Big(y_i - \bar{y} \Big)}{\sqrt{\displaystyle\sum_{i=1}^n \Big(x_i - \bar{x}\Big)^2 \displaystyle\sum_{i=1}^n \Big(y_i - \bar{y}\Big)^2}}
\end{array}\]
The sample correlation coefficient #r# between #X# and #Y# is an unbiased estimate of the population correlation coefficient #\rho# between these two variables.
As with #\rho#, the sample correlation coefficient #r# is between #-1# and #1#, and #r# is unitless.
Moreover, #r# is symmetric, i.e., the sample correlation coefficient between #X# and #Y# is the same as the sample correlation coefficient between #Y# and #X#.
Correlation and the Modification of the VariableThe sample correlation coefficient is unchanged if either variable is modified by the addition of a constant or by multiplication with a constant.
That means that the sample correlation coefficient between #X# and #Y# is the same as the sample correlation coefficient between #aX + b# and #cY + d# for any constants #a,b,c# and #d# with #a \neq 0# and #c \neq 0#.
For example, if one of the variables is length and the other is weight, the correlation coefficients would be the same whether these two variables were measured in centimeters and kilograms, respectively, or measured in inches and pounds.
#\text{}#
A strong correlation between two variables does not imply that changes in the value of one of the variables causes changes in the value of the other variable. It could be that the perceived relationship between the two variables is spurious.
Spurious RelationshipA spurious relationship between two variables indicates that changes in the values of both variables are caused by changes in the values of other unmeasured variables, which we call confounding variables (or lurking variables).
Hence we say that correlation does not imply causation (although causation does imply correlation).
For example, there is a strong positive association between the amount of damage done by a fire and the number of firefighters that are sent to put it out. This does not mean, however, that the firefighters are the cause of the damage.
To illustrate this point, consider the following two statements:
- The larger the fire, the more damage is caused.
- The larger the fire, the more firefighters are sent to put it out.
Here, the size of the fire acts as a lurking variable that influences both the amount of damage done by the fire and the number of firefighters that are sent to put it out, thereby creating a spurious association between the two variables.

The idea behind experimental design is to eliminate the possibility of confounding from other variables, so that causation can be established.
\[\text{}\]
Visual AnalysisBivariate quantitative data can be displayed using a scatterplot, as in the following figure:
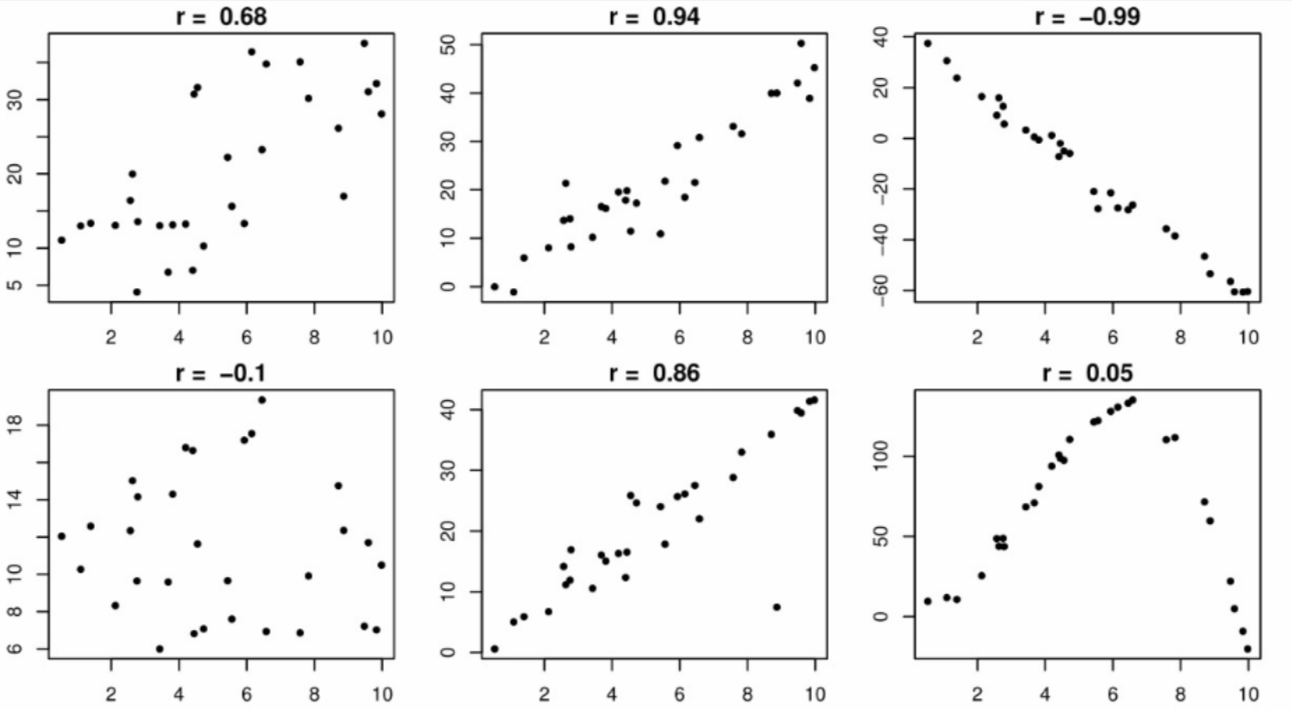
The data in the three plots in the first row of the figure illustrate an increasingly stronger linear association (moving left to right) between two quantitative variables, with the first two associations being positive and the third being negative. This corresponds with the value of the sample correlation coefficient shown above each plot. For the plot in the upper right corner, it is quite easy to visualize a line around which the points are clustered, while a bit less so for the middle plot, and still less for the first plot. In most research settings outside of physics it would be very rare to have two variables whose association is so strong that their scatterplot looks like the plot in the upper right. The plot in the upper left is more typical.
The data in the first plot of the second row show that the two variables have almost no association, and thus a correlation coefficient close to zero. The second panel of the second row shows that the value of #r# can be strongly influenced by a single outlier. The given value for #r# would be much closer to #1# if not for the outlier. Furthermore, it is important to understand that #r# is a measure of the linear association between two variables. The last panel of the second row shows that the two variables have a very obvious nonlinear association, in which case #r# is not an appropriate measure of their association. The correlation coefficient of #0.05# would be very misleading in this case.
Important: When we say “make a scatterplot of variable #A# against variable #B#” we mean that measurements of variable #A# should be on the vertical axis and measurements of variable #B# should be on the horizontal axis.
\[\text{}\]Once we have computed a value for #r#, we would like to make inferences about the population correlation coefficient #\rho#. We may want to know whether or not #\rho# is different from zero, or positive, or negative. We may want to have an estimate of the value of #\rho#.
To make such inferences, we need to make some assumptions about the relationship between the two variables, from which we can estimate the sampling distribution of #r#.
Inference about the Population Correlation CoefficientWe say that the pair of random variables #(X,Y)# has a bivariate normal distribution if the random variable #aX + bY# has a normal distribution for every pair of constants #a# and #b#. A sample from a bivariate normal distribution will result in a scatterplot with an elliptical shape.
In this setting, we can make inference about the population correlation coefficient #\rho# based on the sample correlation coefficient #r#. It can be shown, when the sample size is large, that the statistic \[W = \cfrac{1}{2} \ln \bigg( \cfrac{1 + r}{1 - r}\bigg)\] has an approximate \[N\Bigg(\cfrac{1}{2} \ln \bigg(\cfrac{1 + \rho}{1 - \rho}\bigg),\cfrac{1}{n - 3}\Bigg)\] distribution.
Confidence interval for #\rho#
We can construct a #(1 - \alpha)100\%# CI for #\rho# as follows: \[\Bigg(\cfrac{e^{2(W-z_{\alpha/2}/\sqrt{n-3})} - 1}{e^{2(W-z_{\alpha/2}/\sqrt{n-3})} + 1},\cfrac{e^{2(W+z_{\alpha/2}/\sqrt{n-3})} - 1}{e^{2(W+z_{\alpha/2}/\sqrt{n-3})} + 1}\Bigg)\] The upper bound should not exceed #1#, and the lower bound should not be smaller than #-1#, since we require #-1 \leq \rho \leq 1#.
Hypothesis test about #\rho#
For any #\rho_0 \neq 0#, we can test
#H_0 : \rho = \rho_0# or #H_0 : \rho \leq \rho_0# or #H_0 : \rho \geq \rho_0#
against
#H_1 : \rho \neq \rho_0# or #H_1 : \rho > \rho_0# or #H_1 : \rho < \rho_0#
respectively, as follows:
Set \[W_0 = \cfrac{1}{2} \ln \bigg(\cfrac{1 + \rho_0}{1 - \rho_0}\bigg)\] and compute \[Z = \cfrac{W - W_0}{\sqrt{1/(n - 3)}}\] where \[W = \cfrac{1}{2 }\ln \bigg(\cfrac{1 + r}{1 - r}\bigg)\] Then #Z \sim N(0,1)#.
Depending on the form of #H_1#, compute the P-value using the standard normal distribution as we have done multiple times already.
However, when #\rho_0 = 0#, the procedure to test
#H_0 : \rho = \rho_0# or #H_0 : \rho \leq \rho_0# or #H_0 : \rho \geq \rho_0#
against
#H_1 : \rho \neq \rho_0# or #H_1 : \rho > \rho_0# or #H_1 : \rho < \rho_0#
respectively, is much simpler.
Set \[U = \cfrac{r\sqrt{n-2}}{\sqrt{1 - r^2}}\] Then #U \sim t_{n-2}#.
Depending on the form of #H_1#, compute the P-value using the Student’s t-distribution as we have done many times previously.
AssumptionsThe Pearson sample correlation coefficient is only appropriate when both variables are continuous, and the above CI and hypothesis tests have the further restriction of bivariate normality.
If these restrictions are not satisfied, the Spearman rank correlation coefficient or Kendall’s tau are preferred non-parametric alternatives. We do not cover these methods in this course.
\[\text{}\]
Using RPearson Correlation Coefficient
To compute the Pearson sample correlation coefficient #r# between two variables whose paired measurements are contained in two numerical vectors #X# and #Y# of the same length, we use:
> cor(X,Y)
Two-sided Correlation Test
If you want to conduct a hypothesis test for a non-zero (or positive, or negative) population correlation coefficient #\rho# between paired numeric vectors #X# and #Y# of the same length, you can use:
> cor.test(X,Y)
This function will also output a confidence interval for #\rho#.
One-sided Correlation Test
For a one-sided test, you can specify the form of the alternative, as in the previous hypothesis tests we have discussed, and you can also specify the confidence level of the confidence interval for the population correlation #\rho#. For example:
> cor.test(X, Y, conf.level=0.99, alternative="greater")
Note that this function only performs the version of the test when #\rho_0 = 0#. But the confidence interval can be used to assess whether or not #\rho# differs from some other null value.

Or visit omptest.org if jou are taking an OMPT exam.



