Rekenregels voor differentiëren: Toepassingen van de afgeleide
 Benadering
Benadering
Neem aan dat we geïnteresseerd zijn in de numerieke waarde van #\sqrt{1.1}#. We weten dat de raaklijn in #x=1# aan de grafiek van #\sqrt{x}# een goede benadering geeft. Hieronder zijn de grafiek van de wortel en de raaklijn getekend.
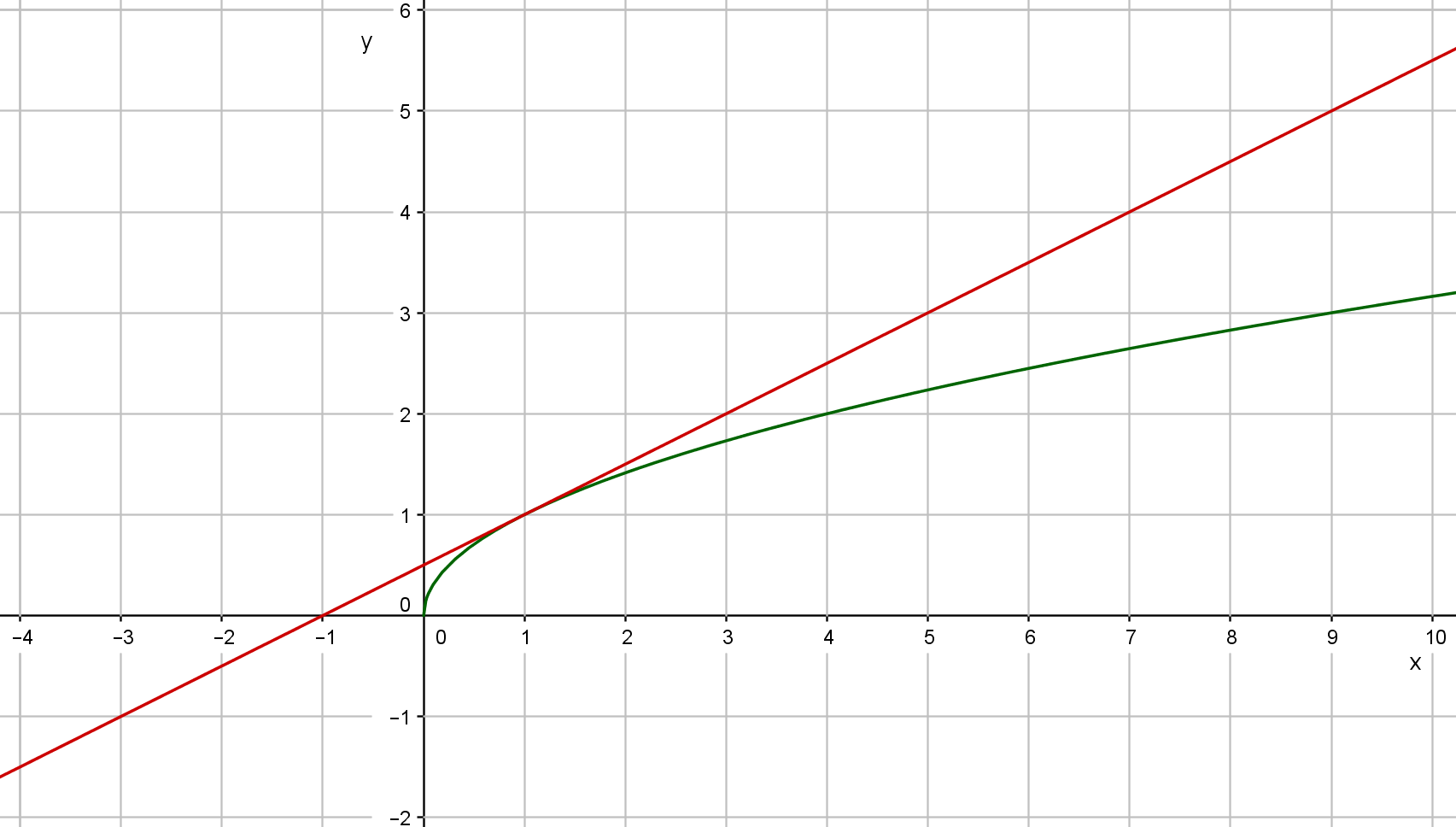
Als we inzoomen op het punt #\rv{1,1}#, dan zien we dat de grafiek van #\sqrt{x}# en de raaklijn, die gegeven is door de functie #\frac{1}{2}x+\frac{1}{2}#, in het punt #x=1# heel dicht bij elkaar liggen; zie de figuur hieronder.
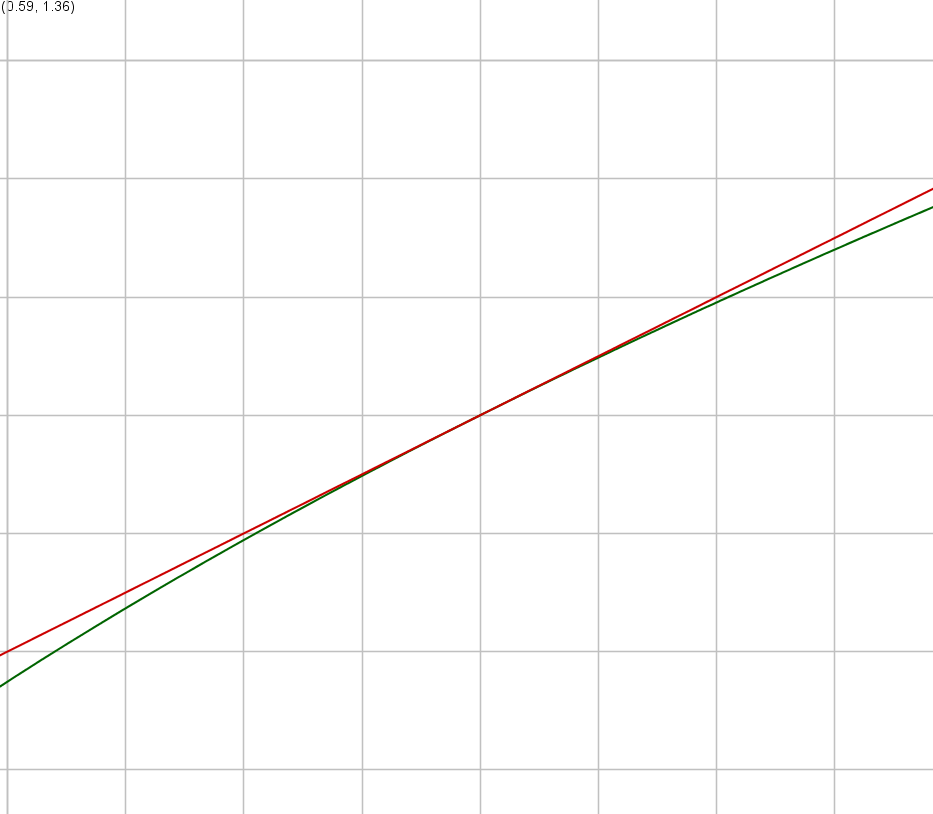
In het bijzonder is de waarde van de functie van de raaklijn in #x=1.1#, het getal #\frac{1}{2} \cdot 1.1+{1}{2}=1.05#, een goede benadering van #\sqrt{1.1}#. Dit is een voorbeeld van de volgende raaklijn benaderingsformule.
Raaklijn benaderingsformule
Laat #a# een punt zijn waar de functie #f# differentieerbaar is. Als #h# dicht genoeg bij #0# gekozen wordt, dan zal #f(a)+f'(a) \cdot h# een goede benadering van #f(a+h)# zijn. In formule:
\[f(a+h)\approx f(a)+f'(a) \cdot h\tiny.\]
Er geldt #f'(a)=\lim_{h \to 0} \frac{f(a+h)-f(a)}{h}# volgens de definitie van de afgeleide.
Dit betekent dat: #f'(a)\approx\frac{f(a+h)-f(a)}{h}#.
Dit geeft: #f(a+h)\approx f(a)+f'(a) \cdot h#.
Er zijn goede afschattingen voor de afwijking van #f(a)+f'(a) \cdot h# ten opzichte van #f(a+h)#, maar daar gaan we hier niet op in.
Met behulp van deze formule kunnen we nu voor een differentieerbare functie de waarde benaderen in punten, waarvoor we anders een rekenmachine nodig hadden.
We gebruiken de raaklijn benaderingsformule. Deze luidt: #f(a+h)\approx f(a)+f'(a) \cdot h#. Hierbij geldt #f(a)=\sqrt{x}#, #a=4.0# en #h=0.10#.
Om te beginnen berekenen we de afgeleide van #f# met behulp van de machtregel voor differentiëren: #f'(x)={{1}\over{2\cdot \sqrt{x}}}#. Nu kunnen we de formule invullen: \[\sqrt{4.10}\approx f(4.0)+f'(4.0)\cdot 0.10 = \sqrt{4.0}+\frac{1}{2 \cdot \sqrt{4.0}} \cdot 0.10\approx 2.0250\tiny.\]
Ter vergelijking: de precieze benadering van #\sqrt{4.10}# tot op vier decimalen is: #2.0248#.

omptest.org als je een OMPT examen moet maken.



