Bewerkingen met functies: Inverse functies
Karakterisering van inverteerbare functies
Karakterisering van inverteerbare functies
Een functie \(f\) heeft dan en slechts dan een inverse als ze injectief is. In dat geval is het domein van #f^{-1}# gelijk aan het bereik van #f#.
Als #f# injectief is, dan heeft de vergelijking #y=f(x)# met onbekende #x# precies één oplossing als #y# in het bereik van #f# ligt en géén oplossing als dat niet het geval is. Dit betekent dat de functie #g# met domein gelijk aan het bereik van #f# en met voorschrift \[g(y)\text{ is de unieke oplossing }x\text{ van }y=f(x)\] de inverse van #f# is.
Andersom: stel dat #g# de inverse van #f# is, en dat #x_1# en #x_2# getallen in het domein van #f# zijn met #f(x_1)=f(x_2)#. Dan moet gelden #x_1=g(f(x_1)=g(f(x_2))= x_2#, ofwel: #x_1=x_2#. Dit laat zien dat #f# injectief is.
De verticale lijn-test voor inverteerbaarheid
Laat #f# een functie zijn.
- De grafiek van #f# snijdt elke horizontale lijn dan en slechts dan hooguit één keer als #f# injectief is.
- De grafiek die je krijgt door de grafiek van #f# om de lijn met vergelijking #x=y# te spiegelen, snijdt elke verticale lijn dan en slechts dan hoogstens één keer als #f# inverteerbaar is.
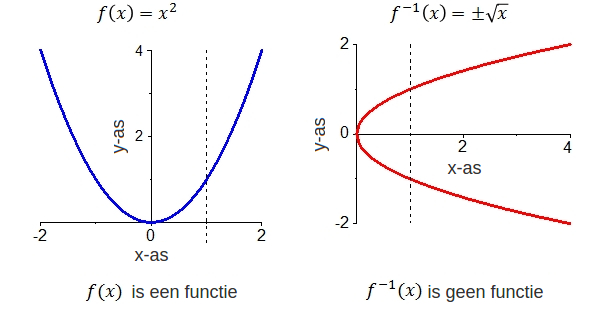
De functie #f(x)=x^2# is hieronder aan de linkerkant afgebeeld en de gespiegelde rechts. Het is duidelijk dat de twee criteria gelijk zijn: Links zijn er horizontale lijnen die de grafiek in twee punten snijden. De functie #f# is dus niet injectief. Rechts zijn er verticale lijnen die de grafiek in twee punten snijden. Deze grafiek behoort dus niet bij een functie; maar het zou de grafiek van de inverse functie moeten zijn; dit laat zien dat #f# geen inverse heeft.
Omdat alle vijf waarden van #f# verschillen, is deze functie injectief, dus inverteerbaar. Wat is de inverse van #f#?
Beschrijf #f^{-1}# door een lijst van vijf getallen als voor #f#.
Kijk naar de waarden van #f # op positie #j#.
#\begin{array}{rcl}
\text{de waarde van } f = & [4,1,5,2,3] \\
\text{op positie } j = & [1,2,3,4,5] \\
\end{array}#
De inverse functie #f^{-1} # wisselt de posities en de waarden van #f#:
#\begin{array}{rcl}
\text{de nieuwe waarde } = & [1,2,3,4,5] \\
\text{op positie } j = & [4,1,5,2,3] \\
\end{array}#
Als we deze lijst van waarden sorteren gebaseerd op de positie, krijgen we
#f^{-1} = [2,4,5,1,3]#
Inderdaad, positie #j# in deze lijst is de positie waar #f# de waarde #j# heeft staan.
Bijvoorbeeld op positie #1#:
#f# zet positie #1# op waarde #4,# dus #f(1)=4#. De inverse functie moet deze verandering ongedaan maken, waardoor #f^{-1}(4)=1#.
Op dezelfde manier voor positie #2#:
Omdat #f(2)=1#, #f^{-1}(1)=2#.
Als deze lijst #g# heet, dan geldt dus #f(g(j)) = j# voor elke #j\in\{1,2,3,4,5\}#. Dit betekent dat #g# het omgekeerde van #f# is en als je eerst #f# toepast, en daarna #f^{-1}#, alles weer in de oorspronkelijke positie staat.
omptest.org als je een OMPT examen moet maken.
