Exponential functions

Operations for functions: Exponential and logarithmic functions

Exponential functions

Exponential functions occur naturally in real life. Consider, for example, the number of bacteria that grow in a culture medium where each minute every bacterium splits into two bacteria. If we start with one bacterium, then after one minute we have two bacteria, after 2 minutes 4 bacteria, and so on:

Time (in minutes)	Number of bacteria
0	1
1	2
2	4
3	8
4	16
5	32

If \(x\) is the number of minutes that have passed and \(y\) is the number of bacteria, the equation that describes the growth is \[y=2^x\tiny.\] Clearly, #y# is a function of #x#. The graph of this function is shown below.

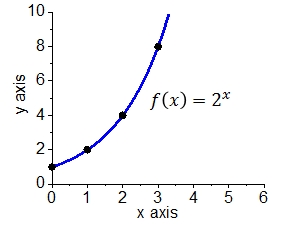
The function \(2^x\) is an of an example of an exponential function:

Exponential function

If \(a\) is a positive real number, then the function \[f(x)= a^x\] is called the exponential function with base \(a\). Its domain is #\mathbb{R}#.

The reason for requiring the base \(a\) to be positive is related to the fact that for negative values of \(a\) the power \(a^x\) is not always defined. For example, if #a=-2# and #x=\frac{1}{2}#, then #a^x=(-2)^{\frac{1}{2}}# is a number squaring to #-2#, but no such number is real.

Later we will see that, if #a\gt1#, the exponential function #a^x# grows faster than any power function.

The function \(f(x)=x^a\), “raising \(x\) to the power \(a\)”, where the independent variable is the base \(x\), is a power function, but not an exponential function.