Bewerkingen met functies: Nieuwe functies uit oude
Translaties van functies
We zullen verschillende manieren van het manipuleren een grafiek in het platte vlak bestuderen. Ook bekijken we de gevolgen in het geval dat de grafiek er een van een functie is. We zullen beginnen met het omhoog of omlaag verschuiven van de grafiek.
Verticale translatie
Laat #a# een reëel getal zijn. De verticale translatie van #a# verplaatst het punt #\rv{x,y}# in het vlak naar #\rv{x,y+a}#.
Laat \(f\) een reële functie zijn. Door de verticale translatie van #a#, wordt de grafiek van #f# omgezet in de grafiek van de functie van #x# met functievoorschrift #f(x)+a#.
De grafiek van de functie \(f\) beweegt omhoog als \(a\gt0\) en naar beneden als \(a\gt0\)\.
De ligging van de nulpunten van de functie \(f\) verandert, maar de locatie van de minima en/of maxima zal niet veranderen in termen van \(x\) maar alleen in termen van \(y\) omdat \(a\) aan de oorspronkelijke waarde wordt toegevoegd.
Bij wijze van voorbeeld tonen we hier twee verticale translaties van de grafiek #f(x)=x^2-1#:
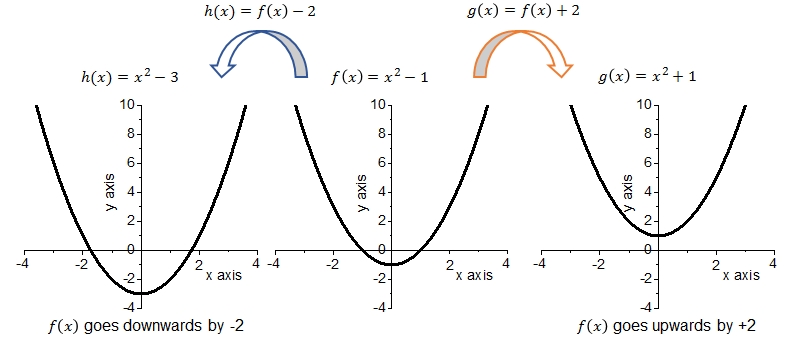
De volgende feiten kunnen worden waargenomen uit deze grafieken:
- De grafiek van \(f\) is een parabool met nulpunten \(x=-1\) en \(x=1\) en heeft een minimum bij \(f(0)=-1\).
- De grafiek van \(h\) is een parabool met nulpunten \(x=\sqrt{3}\) en \(x=-\sqrt{3}\) en heeft een minimum bij \(f(0)=-3\).
- De grafiek van \(g\) is een parabool zonder nulpunten en heeft een minimum bij \(f(0)=1\).
Nu behandelen we het naar links of rechts verschuiven van een grafiek.
Horizontale translatie
Laat #a# een reëel getal zijn. De horizontale translatie van #a# verplaatst het punt #\rv{x,y}# in het vlak naar #\rv{x+a,y}#.
Laat \(f\) een reële functie zijn. Door de horizontale translatie van #a# wordt de grafiek van #f# omgezet in de grafiek van de functie van #x# met functievoorschrift #f(x-a)#.
De functie \(f\) verplaatst naar links als \(a\gt0\) en naar rechts als \(a\lt0\). De locatie van de nulpunten van de functie \(f\) verplaatst in dezelfde richting (door toevoeging van \(a\) aan de waarde van \(x\) ), maar de locatie van de minima en/of maxima zal veranderen in termen van \(x\) omdat \(a\) moet worden toegevoegd aan de oorspronkelijke waarde, maar de \(y\) zal hetzelfde blijven. Bij wijze van voorbeeld tonen we hier twee verticale translaties van de grafiek #f(x)=x^2-1#:
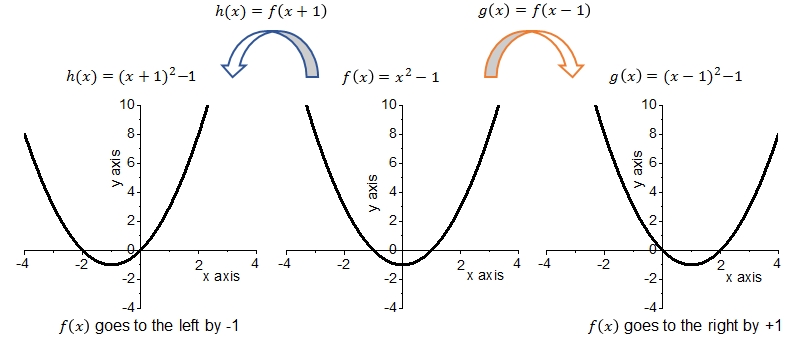
De volgende feiten kunnen worden waargenomen uit deze grafieken:
- De grafiek van \(f\) is een parabool met nulpunten \(x=-1\) en \(x=1\) en heeft een minimum bij \(f(0)=-1\).
- De grafiek van \(h\) is een parabool met nulpunten \(x=-2\) en \(x=0\) en heeft een minimum bij \(f(-1)=-1\).
- De grafiek van \(g\) is een parabool met nulpunten \(x=0\) en \(x=2\) en heeft een minimum bij \(f(1)=-1\).
De verticale translatie van de grafiek hoort bij de functie #3+ f(x) = 3 + \left(\sqrt{x-2}\right)# en de grafiek is rood.
De horizontale translatie van de grafiek hoort bij de functie # f\left({x- 3}\right) = \sqrt{x-5}# en de grafiek is groen.
omptest.org als je een OMPT examen moet maken.
