Functies: Kwadratische functies
De abc-formule
Door kwadraat af te splitsen kunnen we de kwadratische uitdrukking #ax^2+bx+c# herschrijven tot \[a\cdot\left(\left(x+\dfrac{b}{2a}\right)^2-\dfrac{b^2-4a\cdot c}{(2a)^2}\right)\tiny.\] We gebruiken deze splitsing om kwadratische vergelijkingen op te lossen.
Discriminant en abc-formule
Laat #a#, #b#, #c# reële getallen zijn met #a\ne0#. De vergelijking #ax^2+bx+c=0# kan herleid worden tot
\[x=\dfrac{-b - \sqrt{b^2-4a\cdot c}}{2a}\lor x=\dfrac{-b+ \sqrt{b^2-4a\cdot c}}{2a}\]
De uitdrukking #b^2-4ac# noemen we de discriminant van #ax^2+bx+c#, en duiden we vaak aan met #D#.
Met deze notatie geldt\[x=\dfrac{-b - \sqrt{D}}{2a}\lor x=\dfrac{-b+ \sqrt{D}}{2a}\]
- Als #D\lt 0#, dan zijn er geen oplossingen.
- Als #D= 0#, dan is er dus maar één oplossing: #x=\dfrac{-b}{2a}#.
- Als #D\gt 0#, dan zijn er twee oplossingen.
Bovenstaande noemen we ook wel de abc-formule. Met deze formule is elke tweedegraads vergelijking op te lossen.
De herleiding gaat als volgt:
\[\begin{array}{rcl}ax^2+bx+c&=&0\\ &&\phantom{xx}\color{blue}{\text{de oorspronkelijke vergelijking}}\\ a\cdot\left(\left(x+\dfrac{b}{2a}\right)^2-\dfrac{D}{(2a)^2}\right)&=&0\\ &&\phantom{xx}\color{blue}{\text{kwadraat afgesplitst, waarbij }D = b^2-4a\cdot c}\\ \left(x+\dfrac{b}{2a}\right)^2-\dfrac{D}{(2a)^2}&=&0\\ &&\phantom{xx}\color{blue}{\text{links en rechts door }a\text{ gedeeld}}\\ \left(x+\dfrac{b}{2a}\right)^2&=&\dfrac{D}{(2a)^2}\\ &&\phantom{xx}\color{blue}{\text{constante term naar rechts gebracht}}\\ x+\dfrac{b}{2a}&=&\pm\sqrt{\dfrac{D}{(2a)^2}}\\ &&\phantom{xx}\color{blue}{\text{wortel getrokken; }\pm\text{betekent: }+\text{ of }-}\\ x+\dfrac{b}{2a}&=&\pm\dfrac{\sqrt{D}}{2a}\\ &&\phantom{xx}\color{blue}{\text{wortel vereenvoudigd}}\\ x&=&-\dfrac{b}{2a}\pm\dfrac{\sqrt{D}}{2a}\\ &&\phantom{xx}\color{blue}{\text{constante term naar rechts gebracht}}\\ \end{array}\]
De abc-formule gebruiken we om de snijpunten van een parabool met de #x#-as te bepalen. Wat betekent dit voor de drie gevallen die we net hebben gezien? We bekijken nu steeds een dalparabool.
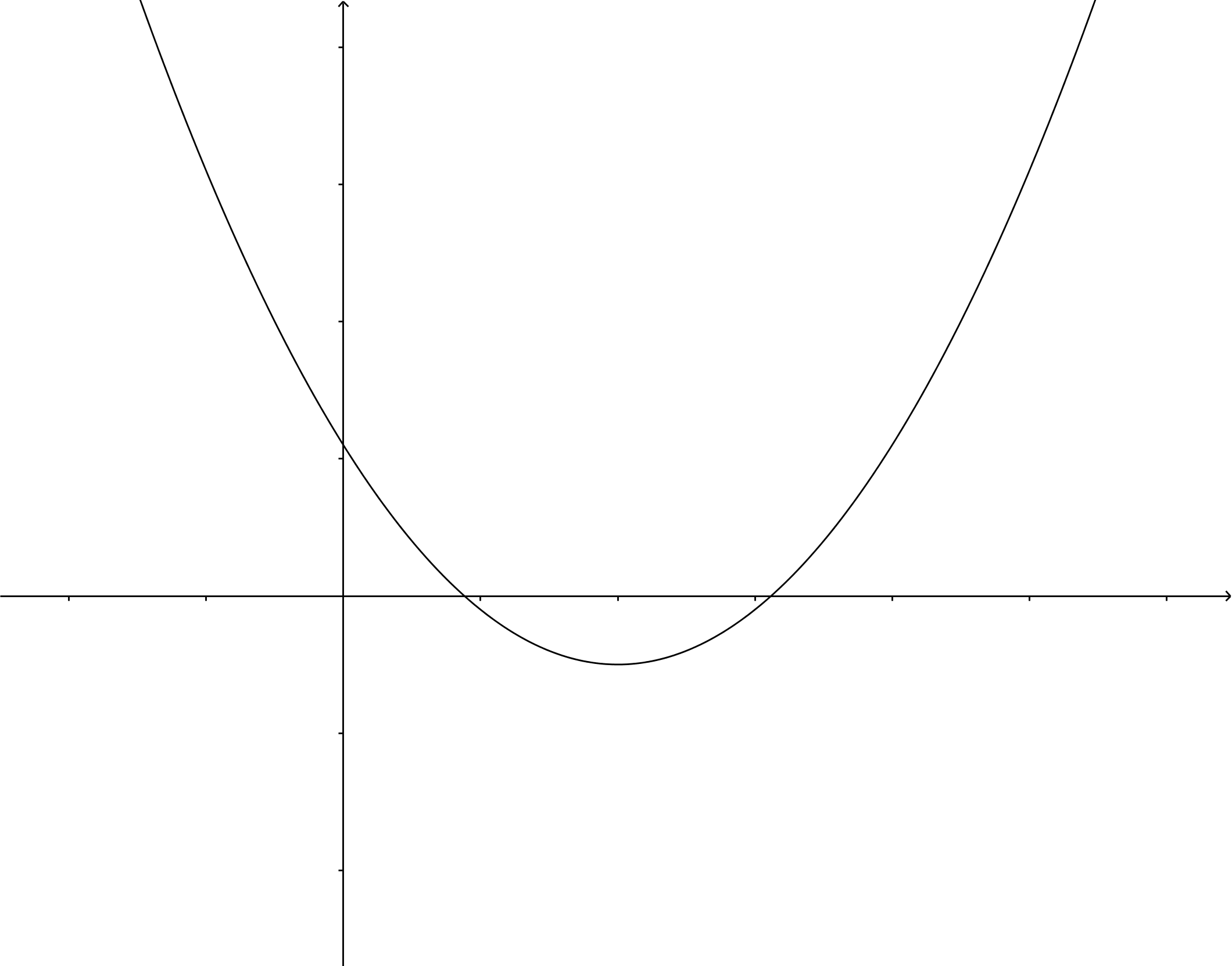
Als #D\gt0#, dan wordt de wortel getrokken uit een positief getal, zodat de vergelijking #ax^2+bx+c=0# twee verschillende oplossingen heeft. De parabool, dat wil zeggen: de grafiek van #ax^2+bx+c#, heeft #2# snijpunten heeft met de #x#-as.
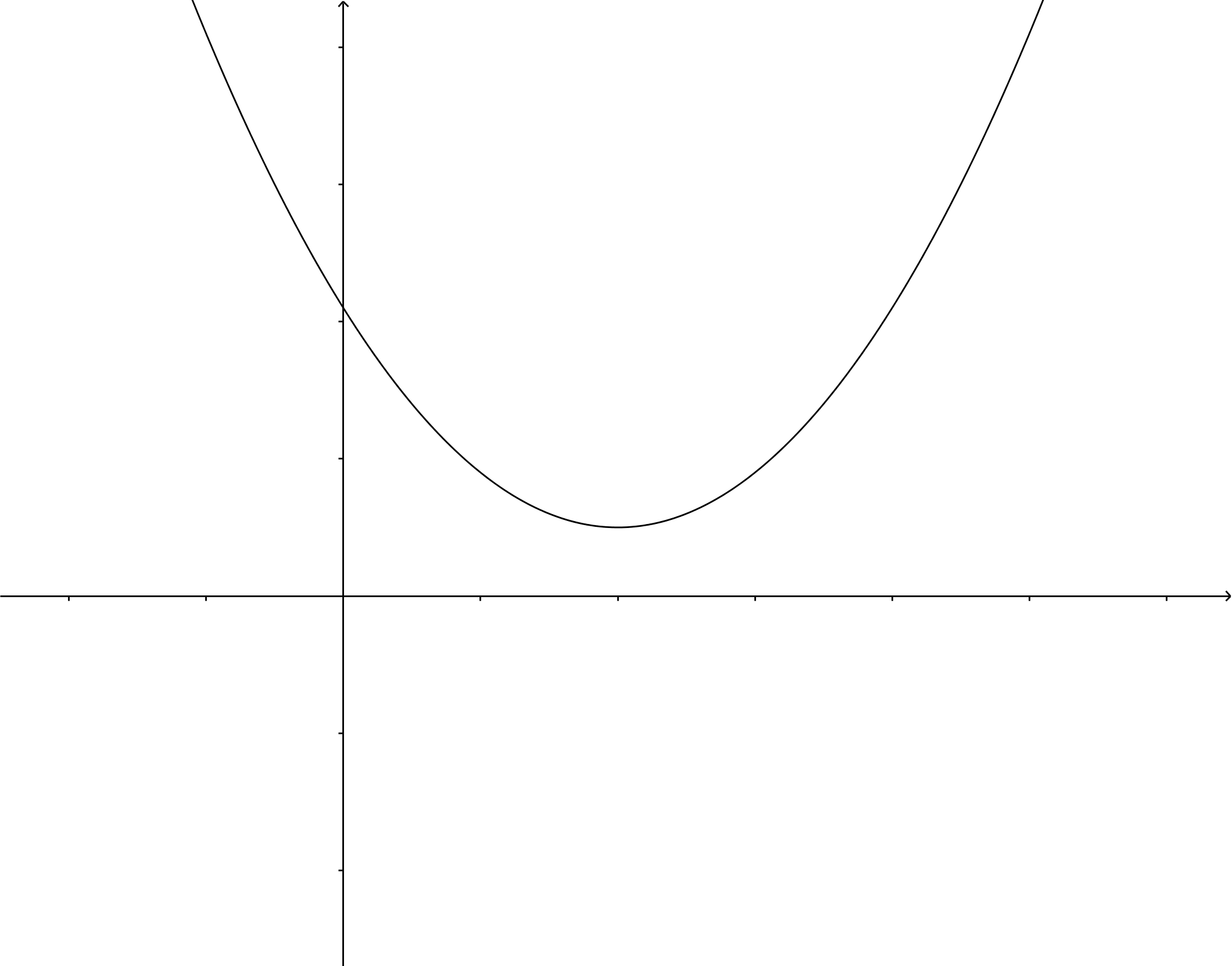
Als #D\lt0#, dan zijn er geen oplossingen, omdat worteltrekken uit een negatief getal geen reëel getal oplevert. De parabool heeft dan geen snijpunten met de #x#-as.
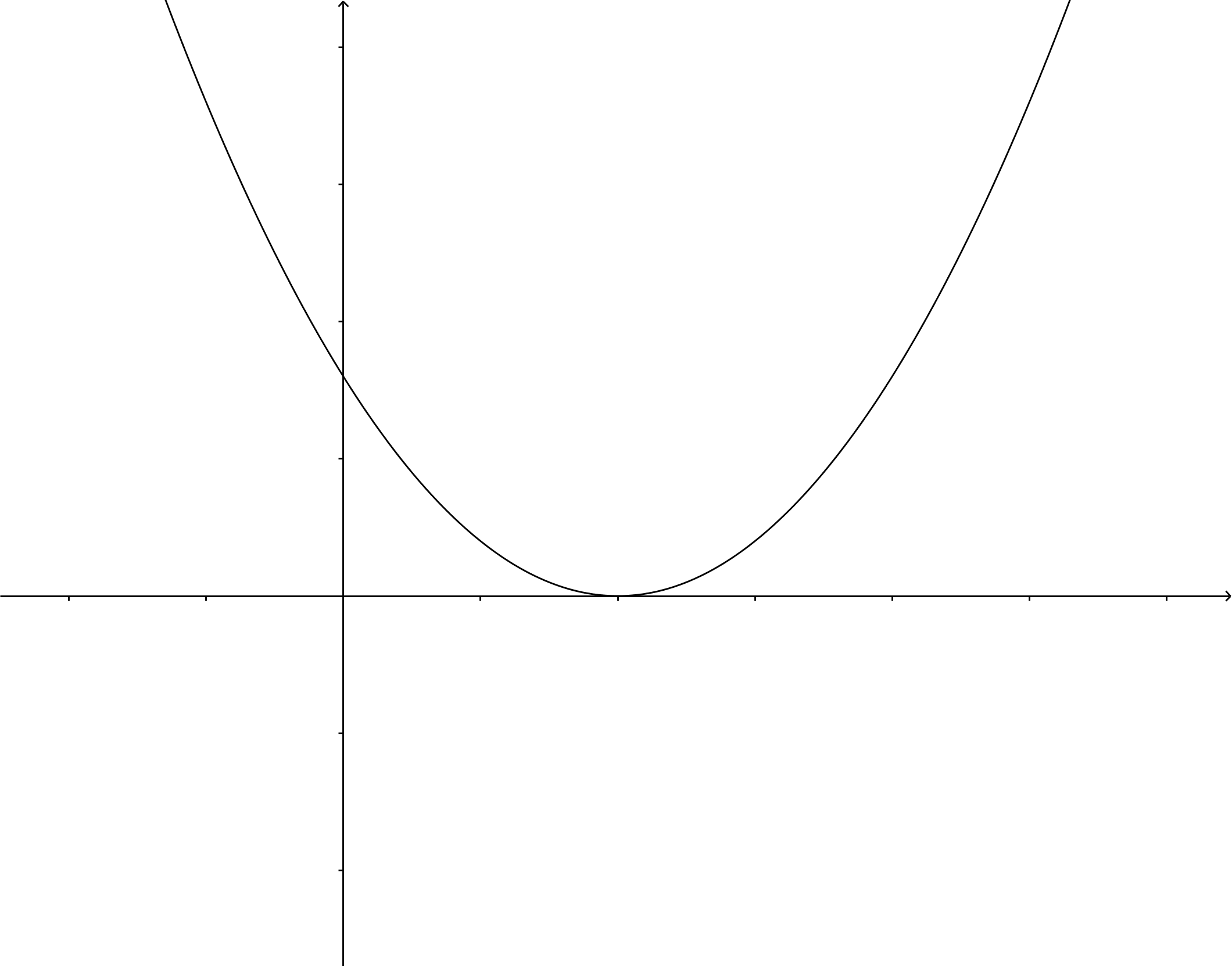
Als #D= 0#, dan zijn beide oplossingen gelijk en is er dus maar één oplossing: #x=\dfrac{-b}{2a}#. Hier raakt de parabool de #x#-as.
Maak gebruik van de abc-formule:
\[x=\frac{-b-\sqrt{D}}{2a}\lor x=\frac{-b+\sqrt{D}}{2a}\]
met discriminant #D=b^2-4a\cdot c#.
\[\begin{array}{rcl}
a=1&b=-2&c=-{{21}\over{4}}\\
&&\phantom{xx}\color{blue}{\text{a, b en c bepaald}}\\
(-2)^2-4\cdot 1\cdot -{{21}\over{4}}&=&25\\
&&\phantom{xx}\color{blue}{\text{discriminant berekend}}\\
x=\frac{2-5}{2}&\lor&x=\frac{2+5}{2}\\
&&\phantom{xx}\color{blue}{\text{abc-formule gebruikt}}\\
x=-{{3}\over{2}}&\lor&x={{7}\over{2}}\\
&&\phantom{xx}\color{blue}{\text{oplossing vereenvoudigd}}\\
\end{array}\]
De grafiek van de functie # x^2-2 x-{{21}\over{4}}# is hieronder getekend. De #x#-coördinaten van de snijpunten van de grafiek met de #x#-as zijn de oplossingen van de vergelijking.
omptest.org als je een OMPT examen moet maken.
