Toepassingen van differentiëren: Functieanalyse
 Monotonie
Monotonie
Monotonie
Laat #f# een functie zijn die gedefinieerd is op een interval #I#.
- #f# heet stijgend als voor alle #c,d\in I# met #c\lt d# geldt #f(c)\lt f(d)#.
- #f# heet dalend als voor alle #c,d\in I# met #c\lt d# geldt #f(c)\gt f(d)#.
- #f# heet zwak stijgend als voor alle #c,d\in I# met #c\lt d# geldt #f(c)\le f(d)#.
- #f# heet zwak dalend als voor alle #c,d\in I# met #c\lt d# geldt #f(c)\ge f(d)#.
De grafiek van een stijgende functie gaat naar rechtsboven.
Aan de hand van de afgeleide valt op te maken of een functie stijgend of dalend is.
Afgeleidecriterium voor monotonie
Stel dat #f# een continue functie is op #I# die differentieerbaar is op het open interval #\ivoo{a}{b}# waar #a# en #b# de randpunten van #I# zijn.
- Als #f'(x)\gt0# voor alle #x\in\ivoo{a}{b}#, dan is #f# stijgend op #I#.
- Als #f'(x)\lt0# voor alle #x\in\ivoo{a}{b}#, dan is #f# dalend op #I#.
- Als #f'(x)\ge0# voor alle #x\in\ivoo{a}{b}#, dan is #f# zwak stijgend op #I#.
- Als #f'(x)\le0# voor alle #x\in\ivoo{a}{b}#, dan is #f# zwak dalend op #I#.
Beschouw de functie \(f(x) = x^4\cdot \euler^ {- 4\cdot x } \). Op welke interval(len) stijgt deze functie?
Schrijf je antwoord in de vorm #a \leq x \leq b# als het slechts één interval is of #(a \leq x \leq b) \lor ( c \leq x \leq d)# als het om twee intervallen gaat. Hierbij zijn #a#, #b#, #c# en #d# exacte getallen.
Gebruik, indien nodig, de waarden van de afgeleide uit onderstaande tabel.
Schrijf je antwoord in de vorm #a \leq x \leq b# als het slechts één interval is of #(a \leq x \leq b) \lor ( c \leq x \leq d)# als het om twee intervallen gaat. Hierbij zijn #a#, #b#, #c# en #d# exacte getallen.
Gebruik, indien nodig, de waarden van de afgeleide uit onderstaande tabel.
| #x# | #-0.5# | #0.5# | #1.0# | #2.0# |
| #f'(x)# | #-5.54# | #0.03# | #0.00# | #-0.01# |
#0\leq x \leq 1#
De functie #f# is stijgend op een interval #I# als #f'(x) \ge 0# voor alle #x# in #I#. De eerste afgeleide van de functie is: \[ f'(x)= 4\cdot x^3\cdot \euler^ {- 4\cdot x }-4\cdot x^4\cdot \euler^ {- 4\cdot x } \tiny. \] Door #x-1# en #x^3# buiten haakjes te halen kunnen we dit herschrijven tot\[f'(x)=-4\cdot \left(x-1\right)\cdot x^3\cdot \euler^ {- 4\cdot x }\tiny.\] De grafiek van deze afgeleide snijdt de #x#-as in #x=0# en #x=1#. Nu kijken we in de tabel om het teken van de afgeleide te bepalen aan weerszijden van de punten #x=0# en #x=1#. Voor #x \ge 0# en #x \le 1#, is #f'(x)# #\text{positief}#, dus stijgt #f(x)# op #\ivcc{0}{1}#, dat wil zeggen: voor # 0\leq x \leq 1#.
Hieronder staat de grafiek van de functie #x^4\cdot \euler^ {- 4\cdot x }#.
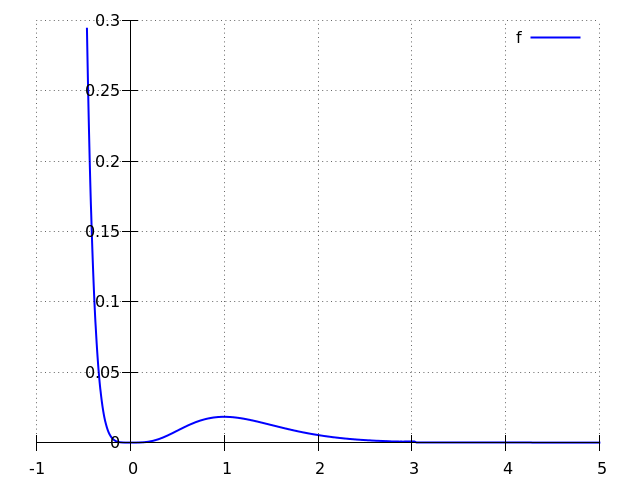
De functie #f# is stijgend op een interval #I# als #f'(x) \ge 0# voor alle #x# in #I#. De eerste afgeleide van de functie is: \[ f'(x)= 4\cdot x^3\cdot \euler^ {- 4\cdot x }-4\cdot x^4\cdot \euler^ {- 4\cdot x } \tiny. \] Door #x-1# en #x^3# buiten haakjes te halen kunnen we dit herschrijven tot\[f'(x)=-4\cdot \left(x-1\right)\cdot x^3\cdot \euler^ {- 4\cdot x }\tiny.\] De grafiek van deze afgeleide snijdt de #x#-as in #x=0# en #x=1#. Nu kijken we in de tabel om het teken van de afgeleide te bepalen aan weerszijden van de punten #x=0# en #x=1#. Voor #x \ge 0# en #x \le 1#, is #f'(x)# #\text{positief}#, dus stijgt #f(x)# op #\ivcc{0}{1}#, dat wil zeggen: voor # 0\leq x \leq 1#.
Hieronder staat de grafiek van de functie #x^4\cdot \euler^ {- 4\cdot x }#.

Ontgrendel volledige toegang


Toegang voor leraar
Vraag een demo account aan. Wij helpen je graag op weg met onze digitale leeromgeving.
Toegang voor student
Is jouw universiteit niet aangesloten?
Via Pass Your Math kan je toegang krijgen tot onze cursussen onafhankelijk van je onderwijsinstelling. Bekijk de prijzen en nog veel meer. Of ga naar
omptest.org als je een OMPT examen moet maken.
omptest.org als je een OMPT examen moet maken.



