Fonctions: Fonctions rationnelles
 Asymptotes et hyperboles
Asymptotes et hyperboles
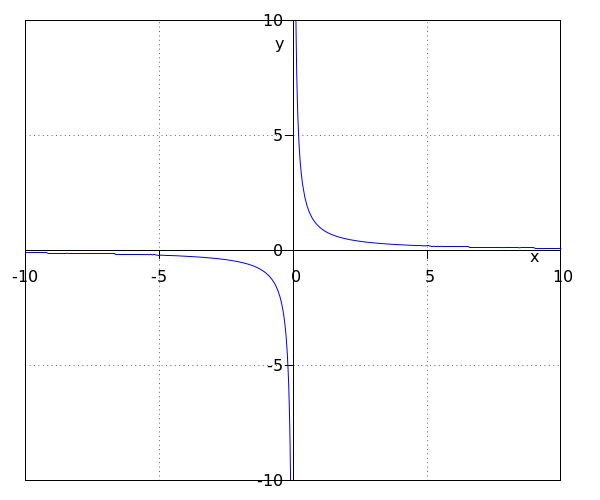
Considérons la fonction #f(x)=\tfrac{1}{x}#. Dans le graphique, nous voyons que le graphe se compose de deux branches. En effet, #0# ne fait pas partie du domaine de la fonction et donc #f(0)# n'existe pas. Nous appelons un tel graphe qui est composé de deux branches une #\blue{\textbf{hyperbole}}#.
Nous constatons que si #x# devient très petit et si #x# devient très grand, alors le graphe se rapproche de l'axe des #x#. Cependant, la valeur de la fonction ne devient jamais égale à #0#. Nous appelons l'axe des #x#, c.-à-d. la droite #y=0#, une #\purple{\textbf{asymptote horizontale}}# au graphe.
Nous constatons de plus que si la valeur de #x# approche la valeur #0# du côté négatif, la valeur de la fonction devient très négative. Le plus proche #x# est de #0#, le plus négatif devient la valeur de la fonction. D'autre part, si la valeur de #x# approche #0# du côté positif, #f(x)# devient très grand. Nous appelons l'axe des #y#, c.-à-d. la droite #x=0#, une #\green{\textbf{asymptote verticale}}# au graphe.
Asymptote et hyperbole
Une asymptote est une droite dont le graphe d'une fonction se rapproche de plus en plus sans jamais la toucher.
Une hyperbole est un graphe d'une fonction qui se compose de deux parties séparées par une asymptote. Ces deux parties sont appelées les branches du graphe.
L'asymptote horizontale est: #y=0#
L'asymptote verticale peut être déterminée en étudiant les valeurs de #x# qui ne peuvent pas être substituées dans la fonction. Pour une fonction rationnel, le dénominateur ne peut pas être égal à #0#. L'asymptote verticale est donc égale à #x=5#.
L'asymptote horizontale peut être déterminée en substituant des valeurs très grandes pour #x# et en étudiant ce qui se passe pour les valeurs de la fonction. Si nous substituons des valeurs très grandes pour #x#, alors #x-5# devient très grand. #{{1}\over{x-5}}# se rapproche de plus en plus de #0#, mais ne devient jamais égale à #0#. L'aysmptote horizontale est donc égale à #y=0#.

Ou visitez omptest.org si jou prenez un examen de OMPT.



