Intersection of parabolas with the axes

Quadratic equations: Drawing parabolas

Intersection of parabolas with the axes

Intersection with the x-axis

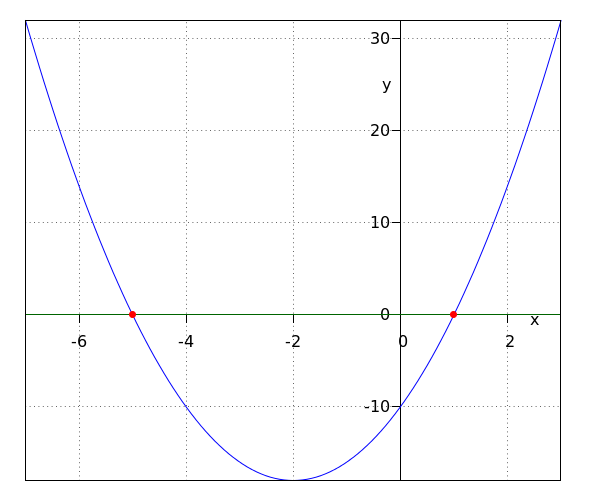
The intersection points of a parabola with the #x#-axis are the points along the graph where #y=0#.

To find the #x# coordinates of these points, equate the formula of the parabola to #0# and solve for #x#:

\[ax^2+bx+c=0\]

This can be done by factorization, completing the square, or using the quadratic formula.

A parabola can have two, one, or no intersections with the #x#-axis.

geogebra picture

Example Consider the parabola #y=2x^2+8x-10#.

The #x# coordinates of the intersections with the #x#-axis can be found by solving the equation: \[2x^2+8x-10=0\]

This is done as follows:

\[\begin{array}{rcl}2x^2+8x-10&=&0 \\ &&\phantom{xx}\blue{\text{the equation to be solved}}\\ x^2+4x-5&=&0 \\ &&\phantom{xx}\blue{\text{divided both sides by }2}\\ \left(x+5\right) \left(x-1\right)&=&0 \\ &&\phantom{xx}\blue{\text{factorized}}\\x+5=0 &\lor& x-1=0 \\ &&\phantom{xx}\blue{A \cdot B \Leftrightarrow A=0 \lor B=0}\\x=-5 &\lor& x=1 \\ &&\phantom{xx}\blue{\text{transferred the constants to the right-hand side}} \end{array}\]

So the intersections of #y=2x^2+8x-10# with the #x#-axis are #\rv{-5,0}# and #\rv{1,0}#.

Intersection with the y-axis

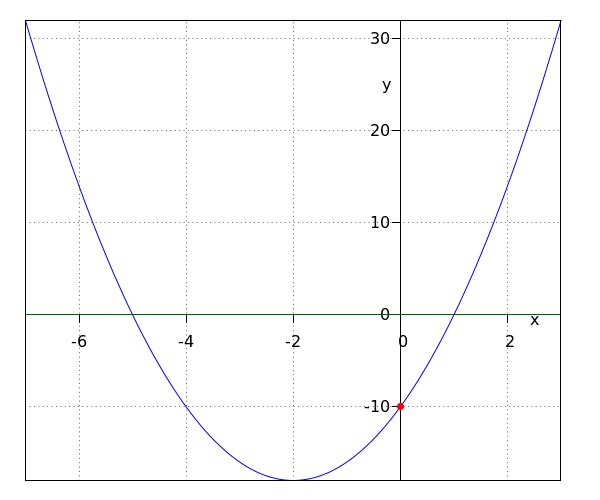
The intersection point of a parabola with the #y#-axis is the point along the graph where #x=0#.

A parabola always has a single point of intersection with the #y#-axis.

To find the #y# coordinate of this point, substitute #0# for #x# in the formula of the parabola.

A parabola described by #y=\blue a x^2+\green b x +\purple c# intersects the #y#-axis at the point #\rv{0,\purple c}#.

geogebra picture

Example Consider the parabola #y=2x^2+8x-10#.

We find the #y# coordinate of the intersection with the #y#-axis by substituting #0# for #x# in the formula.

\[y=2 \cdot 0^2+8 \cdot 0 -10=-10\]

So the the parabola #y=2x^2+8x-10# intersects the #y#-axis at the point #\rv{0,-10}#

To determine the graph with the function
\[y={{x^2}\over{5}}+2\cdot x\]
first draw the intersection point with the #y#-axis.

The intersection point with the #y#-axis is equal to the value of the constant in the quadratic function: #0#. Hence, the coordinates of the intersection point with the #y#-axis are: #\rv{0,0}#.

New example