Transformations de fonctions trigonométriques

Trigonométrie: Fonctions trigonométriques

Transformations de fonctions trigonométriques

Nous avons étudié les fonctions sinus et cosinus. Nous pouvons également transformer ces fonctions.

Transformations

Nous pouvons transformer les fonctions $f(x)=\sin(x)$ et $g(x)=\cos(x)$ de quatre manières différentes. Nous le montrerons pour la fonction sinus, mais les mêmes transformations s'appliquent pour la fonction cosinus.

	Transformations	Exemples
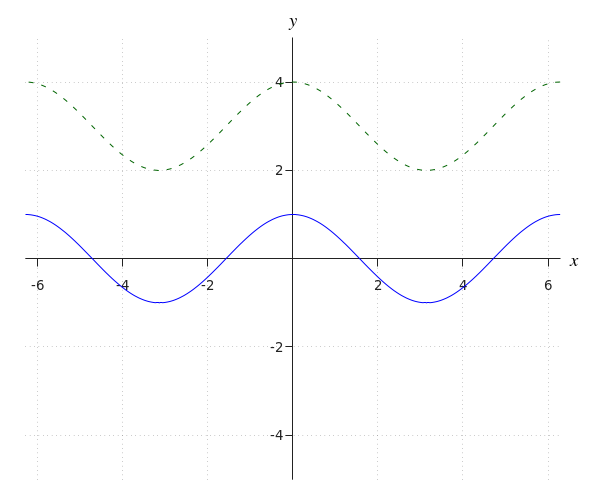
1	Nous déplaçons le graphe de $f(x)=\sin(x)$ de $\green q$ unités vers le haut. La nouvelle fonction devient $f(x)=\sin(x)+\green q$ La période et l'amplitude de la fonction restent les mêmes, mais l'équilibre devient égal à $\green q$ .	Plaatje translatie verticale
2	Nous déplaçons le graphe de $f(x)=\sin(x)$ de $\blue p$ unités vers la droite. La nouvelle fonction devient $f(x)=\sin\left(x-\blue p\right)$ La période, l'amplitude et l'équilibre restent les mêmes. Nous appelons $\blue p$ le déphasage ou la différence de phase.	Plaatje translatie horizontale
3	Nous étirons le graphe de $f(x)=\sin(x)$ en multipliant par $\purple a$ . La nouvelle fonction devient $f(x)=\purple a \sin(x)$ La période et l'équilibre restent les mêmes, mais l'amplitude devient égale à $\purple{\left\| a \right\|}$ . Si $\purple a \lt 0$ , alors le graphe est inversé. Cela signifie qu'il est d'abord décroissant puis croissant. Si $\purple a =- 1$ , la nouvelle fonction est le symétrique de l'ancien graphe par rapport à l'axe des $x$ .	Plaatje vermenigvuldiging x-as
4	Nous étrions le graphe de $f(x)=\sin(x)$ en multipliant par $\orange b$ . Cela signifie que nous remplaçons $x$ par $\frac{1}{\orange b}x$ . La nouvelle fonction devient $f(x)=\sin\left(\frac{1}{\orange b}x\right)$ L'équilibre et l'amplitude restent les mêmes, mais la période devient égale à $\orange b \cdot 2 \pi$ .	Plaatje vermenigvuldiging $y$ -comme.

Plusieurs transformations

Nous pouvons également appliquer plusieurs transformations.

Par exemple: Pour $f(x)=\purple3 \sin\left(x-\blue4\right)$ , nous déplaçons d'abord le graphe de $\blue4$ unités vers la droite et ensuite nous étirons le graphe obtenu en multipliant les ordonnées des points par $\purple3$ .

Composition des fonctions sinus et cosinus

de $f(x)=\purple a \sin(\tfrac{1}{\orange b}(x-\blue p))+\green q$ .

Cette fonction a pour période $\orange b \cdot 2 \pi$ , amplitude $\purple a$ , équilibre $\green q$ et déphasage $\blue p$ .

est de la forme $f(x)=\purple a \cos(\tfrac{1}{\orange b}(x-\blue p))+\green q$ .

Cette fonction a pour période $\orange b \cdot 2 \pi$ , amplitude $\purple a$ , équilibre $\green q$ et déphasage $\blue p$ .

Nous notons que nous pouvons obtenir le cosinus à partir du sinus. Auparavant, nous avons vu que $\cos(x)=\sin(x+\frac{\pi}{2})$

Considérez les deux graphes.

Le graphe bleu correspond à l'équation:
$y=\sin \left(x\right)$
Quelle est l'équation du graphe vert?

$y=$ $\sin \left(x+3\right)$

À l'étape 1, nous avons vu que le graphe vert est obtenu en déplaçant le graphe bleu de $3$ unités vers la gauche. Ainsi, nous remplaçons toutes les occurences de $x$ dans l'expression du graphe bleu $y=\sin \left(x\right)$ par $x+3$ . Nous obtenoons l'équation suivante pour le graphe vert:
$y=\sin \left(x+3\right)$

Nouveau exemple