Characterizing invertible functions

Operations for functions: Inverse functions

Characterizing invertible functions

Characterization of invertible functions

A function $f$ has an inverse if and only if it is injective. In that case the domain of $f^{-1}$ is equal to the range of $f$ .

If $f$ is injective, then the equation $y=f(x)$ with unknown $x$ has exactly one solution if $y$ lies in the range of $f$ and no solution if that is not the case. This means that the function $g$ with domain equal to the range of $f$ and with function rule

$g(y)\text{ is the unique solution }x\text{ of }y=f(x)$ is the inverse of $f$ .

The other way around: assume that $g$ is the inverse of $f$ , and that $x_1$ and $x_2$ are numbers in the domain of $f$ with $f(x_1)=f(x_2)$ . Then $x_1=g(f(x_1)=g(f(x_2))= x_2$ has to hold, or: $x_1=x_2$ . This shows that $f$ is injective.

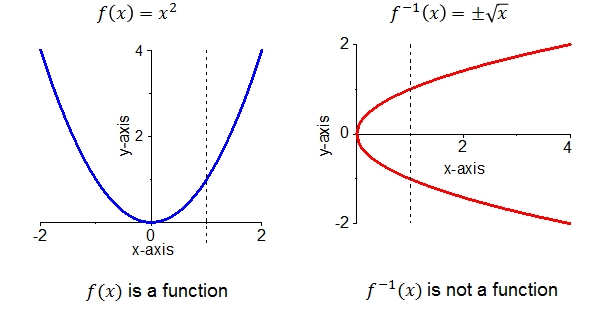
The vertical-line test for invertibility

Let $f$ be a function.

The graph of $f$ meets each horizontal line at most once if and only if $f$ is injective.
The graph obtained by reflecting the graph of $f$ about the line with equation $x=y$ meets every vertical line at most once if and only if $f$ is invertible.

The graph of the function $f(x)=x^2$ is drawn on the left and its reflection about $x=y$ on the right. It is clear that the two criteria are the same: On the left, there are horizontal lines that meet the graph in two points. Therefore, $f$ is not injective. On the right there are vertical lines that meet the graph in two points. Therefore, this graph is not the graph of a function; but it should be the graph of an inverse function. This shows that $f$ has no inverse.

The function $f$ with domain $\{1,2,3,4,5\}$ is described by

$f=[2,4,3,5,1]$ The meaning of the notation is as follows: for every $j\in\{1,2,3,4,5\}$ , the value $f(j)$ is equal to the value at position $j$ in this list. For example $f(2)$ is equal to the value at the second position, hence $f(2) = 4$ .

Because all five values of $f$ differ, this function is injective, and hence invertible. What is the inverse of $f$ ?

Describe $f^{-1}$ by a list of five numbers as was done for $f$ .

$f^{-1}=$ $[5,1,3,2,4]$

Have a look at the values for $f$ at position $j$ .

$\begin{array}{rcl} \text{the value of } f = & [2,4,3,5,1] \\ \text{where position } j = & [1,2,3,4,5] \\ \end{array}$

the inverse function $f^{-1}$ swaps the positions and the values of $f$ :

$\begin{array}{rcl} \text{the new value } = & [1,2,3,4,5] \\ \text{where the position } j = & [2,4,3,5,1] \\ \end{array}$

If we sort the this list of values based on the position, we get
$f^{-1} = [5,1,3,2,4]$

Indeed, position $j$ in this list is the position where $f$ has value $j$ .
As an example for position $1$ :
$f$ has at position $1$ the value $2,$ thus $f(1)=2$ . The inverse function should undo this change, thus $f^{-1}(2)=1$ .

Same way for position $2$ :
Since $f(2)=4$ , $f^{-1}(4)=2$ .

If this list is called $g$ , then $f(g(j)) = j$ holds for each $j\in\{1,2,3,4,5\}$ . This means that $g$ is the inverse of $f$ and if you first apply $f$ , next $f^{-1}$ , all is back into the original positions.

New example