Het begrip inverse functie

Bewerkingen met functies: Inverse functies

Het begrip inverse functie

De omgekeerde van een operatie speelt een grote rol in de wiskunde. Bijvoorbeeld voor optellen is er aftrekken en voor vermenigvuldigen is er deling. Hetzelfde kan worden toegepast op een reële functie. In de figuur staat een functie $f$ afgebeeld met domein $\{1,2,3\}$ en bereik $\{2,4,8\}$ . De functie kun je zien als operatie die het getal $1$ afbeeldt op $2$ , het getal $2$ op $4$ , en het getal $3$ op $8$ .

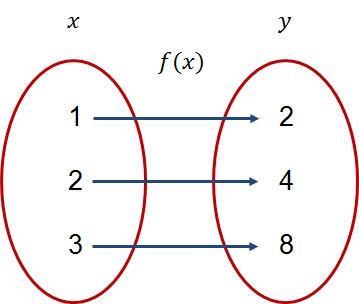
De inverse operatie, dat wil zeggen: de functie die het getal $2$ afbeeldt op $1$ , het getal $4$ op $2$ , en het getal $8$ op $3$ , wordt de inverse functie: $f^{-1}$ . De functie is afgebeeld in onderstaande figuur.

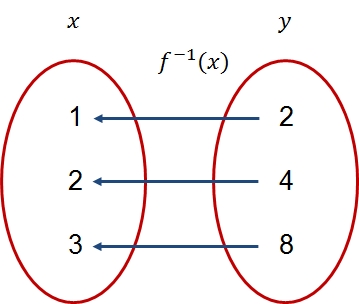
Inverse functie

Laat $f$ en $g$ twee functies zijn, zodat het bereik van elke van de twee gelijk is aan het domein van de ander. Bekijk de volgende twee voorwaarden:

$f(g(y))=y$ voor elke $y$ in het domein van $g$
$g(f(x))=x$ voor elke $x$ in het domein van $f$

Als aan deze twee voorwaarden is voldaan, dan heet $g$ de inverse van $f$ en $f$ de inverse van $g$ . De inverse functie van $f$ wordt aangeduid als $f^{-1}$ ; spreek uit: $f$ -invers.

Als $f$ een functie is waarvoor een inverse bestaat, dan heet $f$ inverteerbaar.

De inverse functie $f^{-1}$ van $f$ voldoet aan $f^{-1}(f(x))=x$ en $f(f^{-1}(y))=y$ en voor alle $x$ in het domein van $f$ en alle $y$ in het bereik van $f$ .

Niet elke functie is de inverse van een functie. Bijvoorbeeld de functie $f$ met domein $\mathbb{R}$ en voorschrift $f(x)=x^2$ heeft geen inverse. Want als $g$ haar inverse zou zijn, dan zou ze moeten voldoen aan $g(x^2)=x$ voor elke $x\in\mathbb{R}$ . Maar voor $x=-1$ en $x=1$ is het linker lid hetzelfde, zodat $-1=g((-1)^2)=g(1)=1$ , een tegenspraak. Dus $f$ heeft geen inverse en is dus ook niet de inverse van een andere functie.

Als we echter het domein van de functie beperken $f$ tot de niet-negatieve reële getallen $\mathbb{R}_{\ge0}$ (en hetzelfde functievoorschrift houden), dan is de functie $g(x)=\sqrt{x}$ de inverse.

We zullen snel de vereisten leren kennen voor het bestaan van de inverse van een gegeven functie.

We spreken van "de" inverse, omdat er hooguit één inverse van een gegeven functie $f$ kan zijn: als $g$ en $h$ beide voldoen aan de definitie van inverse van $f$ , dan geldt:

$\begin{array}{rcl} h(y) &=& h(f(g(y))\\ &&\phantom{xx}\color{blue}{y=f(g(y))}\\ &=& g(y)\\ &&\phantom{xx}\color{blue}{h(f(x))=x\text{ met } x=g(y)} \end{array}$

zodat inderdaad $h=g$ .

De grafiek van een functie $f$ kan duidelijk maken of $f$ een inverse heeft:

Berekening van de inverse functie

Laat $f$ een functie zijn.

Stel dat $g$ een functie is waarvan het bereik samenvalt met het domein van $f$ en het domein samenvalt met het bereik van $f$ . De functie $f$ is dan en slechts dan de inverse van $g$ als ten minste één van de twee gelijkheden uit de definitie van inverteerbaarheid geldt.

Stel $f$ is een inverteerbare functie en $x$ behoort tot het domein van $f$ .

Het beeld $y=f(x)$ van $x$ voldoet aan $x=f^{-1}(y)$ .
De grafiek van $f^{-1}$ is dan uit de grafiek van $f$ te verkrijgen door deze te spiegelen om de lijn met vergelijking $y=x$ .

Stel dat voor $f$ en $g$ de eerste gelijkheid van de definitie van inverse functie geldt: $f(g(y))=y$ voor alle $y$ in het domein van $g$ (en dus het bereik van $f$ ). We bewijzen de tweede gelijkheid van de definitie. Laat $x$ een punt in het domein van $f$ zijn. Dan ligt $x$ in het bereik van $g$ , dus is er een punt $u$ in het domein van $g$ , zodat $x=g(u)$ . Nu kunnen we $g(f(x))$ als volgt herschrijven:

$\begin{array}{rcl}g(f(x))&=& g(f((g(u)))=g(u)=x\end{array}$ Hiermee is de tweede gelijkheid afgeleid.

De afleiding van de eerste gelijkheid van de definitie uit de tweede gaat net zo.

Stel nu dat $f$ inverteerbaar is. We bekijken de uitspraken uit de opsomming.

Als $y=f(x)$ , dan geldt $x=f^{-1}(f(x)) =f^{-1}(y)$ . Dit bewijst de eerste uitspraak uit de opsomming.

Spiegeling om de lijn met vergelijking $x=y$ voert het punt $\rv{x,f(x)}$ van de grafiek van $f$ over in het punt $\rv{f(x),x}=\rv{y,f^{-1}(y)}$ : een punt van de grafiek van $f^{-1}$ . Dit verklaart de tweede uitspraak uit de opsomming.

Als voorbeeld zijn de grafieken van de functie $f(x)=x^2$ met domein $\ivoo{0}{\infty}$ en van haar inverse, de functie $f^{-1}(x)=\sqrt{x}$ , hieronder getekend.

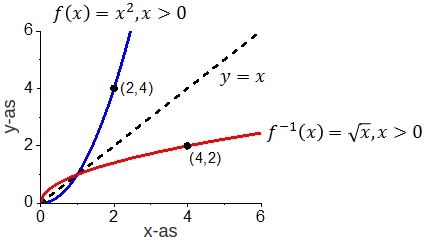
Een andere manier om de grafiek van $f^{-1}$ in termen van de grafiek van $f$ te beschrijven is de volgende:

teken de grafiek van $f$ op een stuk transparant papier;
draai het papier $90^{\circ}$ tegen de klok in (naar links) te draaien;
keer het papier vervolgens om.

De grafiek die zo ontstaat, is de grafiek van $f^{-1}$ . Hieronder is het voorbeeld $f(x)=x^2$ weer getekend, maar nu met de zojuist aangegeven stappen om de inverse te vinden.

De functie $f(x)=x-6$ met domein $\mathbb{R}$ is inverteerbaar. Wat is de inverse functie?

$f^{-1}(x)=$ $x+6$

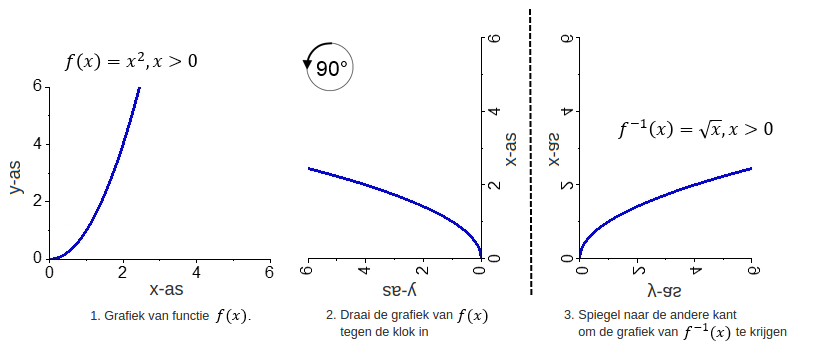
Dit is eenvoudig na te gaan: de functie $g$ met voorschrift $g(x)=x+6$ voldoet aan de twee eisen voor de inverse:

$f(g(y))=f(y+6)=y+6-6=y$
$g(f(x)) = g(x-6) = x-6+6 = x$

Vanwege de stelling Berekening van de inverse functie hoeven we eigenlijk maar één van de twee gelijkheden na te gaan.

Dus $g=f^{-1}$ .

We beschrijven nog hoe je deze inverse functie kunt vinden. Daartoe gaan we uit van de vergelijking $y=f(x)$ waaruit we $x$ oplossen:
$\begin{array}{rcl} y&=& x-6\\ &&\phantom{xx}\color{blue}{\text{het functievoorschrift}}\\ x -6 &=& y\\ &&\phantom{xx}\color{blue}{\text{ links en rechts verwisseld}}\\ x&=& \displaystyle y+6\\ &&\phantom{xx}\color{blue}{\text{links en rechts }-6\text{ afgetrokken}} \end{array}$
Met behulp van de regel Berekening van de inverse functie concluderen we dat $f^{-1}(y)= y+6$ . Het antwoord wordt nu verkregen door het argument $x$ te noemen in plaats van $y$ .

Nieuw voorbeeld