Exponential functions

Operations for functions: Exponential and logarithmic functions

Exponential functions

Exponential functions occur naturally in real life. Consider, for example, the number of bacteria that grow in a culture medium where each minute every bacterium splits into two bacteria. If we start with one bacterium, then after one minute we have two bacteria, after 2 minutes 4 bacteria, and so on:

Time (in minutes)	Number of bacteria
0	1
1	2
2	4
3	8
4	16
5	32

If $x$ is the number of minutes that have passed and $y$ is the number of bacteria, the equation that describes the growth is

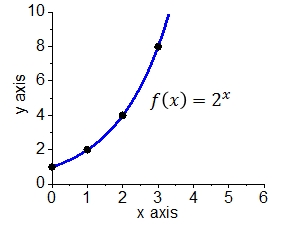
$y=2^x\tiny.$ Clearly, $y$ is a function of $x$ . The graph of this function is shown below.

The function $2^x$ is an of an example of an exponential function:

Exponential function

If $a$ is a positive real number, then the function

$f(x)= a^x$ is called the exponential function with base $a$ . Its domain is $\mathbb{R}$ .

The reason for requiring the base $a$ to be positive is related to the fact that for negative values of $a$ the power $a^x$ is not always defined. For example, if $a=-2$ and $x=\frac{1}{2}$ , then $a^x=(-2)^{\frac{1}{2}}$ is a number squaring to $-2$ , but no such number is real.

Later we will see that, if $a\gt1$ , the exponential function $a^x$ grows faster than any power function.

The function $f(x)=x^a$ , “raising $x$ to the power $a$ ”, where the independent variable is the base $x$ , is a power function, but not an exponential function.