Monotonicity

Applications of differentiation: Analysis of functions

Monotonicity

Monotony

Let $f$ be a function which is defined on an interval $I$ .

$f$ is called increasing if, for all numbers of $c$ , $d$ in $I$ with $c\lt d$ , we have $f(c)\lt f(d)$ .
$f$ is called decreasing if, for all numbers $c$ , $d$ in $I$ with $c\lt d$ , we have $f(c)\gt f(d)$ .
$f$ is called weakly increasing if, for all numbers $c$ , $d$ in $I$ with $c\lt d$ , we have $f(c)\le f(d)$ .
$f$ is called weakly decreasing if, for all numbers $c$ , $d$ in $I$ with $c\lt d$ , we have $f(c)\ge f(d)$ .

A function that is only increasing or only decreasing is called monotonic.

The graph of an increasing function moves to the top right.

By looking at the derivative of a function we can find out if it is increasing or decreasing.

Derivative criterion for monotony

Assume that $f$ is a continuous function on $I$ which is differentiable on the open interval $\ivoo{a}{b}$ where $a$ and $b$ are the boundary points of $I$ .

If $f'(x)\gt0$ for all $x\in\ivoo{a}{b}$ , then $f$ is increasing on $I$ .
If $f'(x)\lt0$ for all $x\in\ivoo{a}{b})$ , then $f$ is decreasing on $I$ .
If $f'(x)\ge0$ for all $x\in\ivoo{a}{b}$ , then $f$ is weakly increasing on $I$ .
If $f'(x)\le0$ for all $x\in\ivoo{a}{b}$ , then $f$ is weakly decreasing on $I$ .

Consider the function $f(x) = x^8\cdot \euler^ {- 4\cdot x }$ . On which interval(s) is this function increasing?

Write your answer in the form $a \leq x \leq b$ if there is only one interval, or $(a \leq x \leq b) \lor ( c \leq x \leq d)$ in the case of two intervals. Here, $a$ , $b$ , $c$ , and $d$ are exact numbers.

Use, if necessary, the values of the derivative from the sign diagram below.

$x$	$-0.5$	$1.0$	$2.0$	$3.0$
$f'(x)$	$-0.58$	$0.07$	$0.00$	$-0.05$

$0\leq x \leq 2$

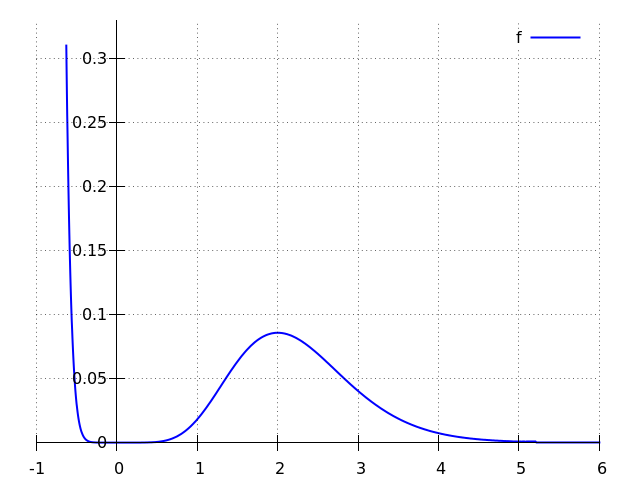
The function $f$ is increasing on an interval $I$ if $f'(x) \ge 0$ for all $x$ in $I$ . The first derivative of the function is:

$f'(x)= 8\cdot x^7\cdot \euler^ {- 4\cdot x }-4\cdot x^8\cdot \euler^ {- 4\cdot x } \tiny.$ By moving $x-2$ and $x^7$ outside of the brackets, we can rewrite this to

$f'(x)=-4\cdot \left(x-2\right)\cdot x^7\cdot \euler^ {- 4\cdot x }\tiny.$ The graph of this derivative intersects the $x$ -axis in $x=0$ and $x=2$ . Now we take a look at the sign diagram to determine the sign of the derivative on both sides of the points $x=0$ and $x=2$ . For $x \ge 0$ and $x \le 2$ , the value $f'(x)$ is $\text{positive}$ , so $f(x)$ is increasing on $\ivcc{0}{1}$ ; in other words, for $0\leq x \leq 2$ .

Below the graph of the function $x^8\cdot \euler^ {- 4\cdot x }$ is drawn.

New example