Lijnen in het vlak

Stelsels lineaire vergelijkingen en matrices: Stelsels lineaire vergelijkingen

Lijnen in het vlak

Een van de vele manieren om een rechte lijn in het platte vlak te beschrijven is een lineaire vergelijking. We bespreken hoe we lineaire vergelijkingen kunnen gebruiken om voor een lijn door twee punten en om de snijpunten van twee lijnen te bepalen.

Een vergelijking voor een lijn in het platte vlak

Laat \(a\), \(b\), en \(c\) vast gekozen reële getallen zijn. De oplossing van de vergelijking \(a\cdot x+b\cdot y+c=0\) kun je in het platte vlak tekenen. Als tenminste één van #a#, #b# ongelijk is aan #0#, dan vormen die punten een rechte lijn, kortweg lijn.

Als \(b\ne0\), dan kunnen we de vergelijking schrijven als \(y=-\frac{a}{b}x-\frac{c}{b}\). Immers, dit zijn de oplossingen als we \(x\) als parameter beschouwen en \(y\) als onbekende. Het geeft aan dat er voor elke waarde van \(x\) een punt \(\rv{x,y}\) is met \(y\) gelijk aan \(-\frac{a}{b}x-\frac{c}{b}\).
- Als \(a \ne 0\) is sprake van een scheve lijn.
- Als \(a=0\), dan is de waarde van \(y\) altijd gelijk aan \(-\frac{c}{b}\), en is sprake van een horizontale lijn.
In het uitzonderingsgeval \(b=0\) ziet de vergelijking er uit als \(a\cdot x+c=0\).
- Als \(a \ne 0\) is sprake van een verticale lijn.
- Als \(a=0\) en
  - \(c\ne 0\) dan zijn er geen oplossingen;
  - \(c=0\) dan is elke waarde voor \(x\) en elke waarde voor \(y\) een oplossing.

Niet uniek

We spreken van een vergelijking van een lijn omdat er meer vergelijkingen mogelijk zijn: voor elk getal \(k\ne 0\) beschrijven de vergelijkingen \(a\cdot x+b\cdot y+c=0\) en \((k\cdot a)\cdot x+(k\cdot b)\cdot y+(k\cdot c)=0\) dezelfde rechte lijn. Met andere woorden: de drietallen \(\rv{a,b,c}\) en \(\rv{k\cdot a,k\cdot b,k\cdot c} \) beschrijven dezelfde rechte lijn.

Parameter

Bij de schrijfwijze \(y=-\frac{a}{b}x-\frac{c}{b}\) spreken we over #x# als parameter. Dit komt overeen met de parametervoorstelling \(\rv{x,y}=\rv{x,-\frac{a}{b}x-\frac{c}{b}}\) die in een eerder hoofdstuk besproken is.

Niet alleen de lijnen zelf zijn oplossingen van lineaire vergelijkingen, ook het bepalen van snijpunten van lijnen en het vinden van een lijn door twee punten is terug te voeren tot het oplossen van lineaire vergelijkingen:

Bewerkingen met lijnen in het vlak

Het opsporen van snijpunten van twee lijnen staat gelijk aan het vinden van de oplossingen van het stelsel vergelijkingen van de bijbehorende lijnen.
Een vergelijking voor de lijn door twee verschillende punten #\rv{p,q}# en #\rv{r,s}# is te vinden door een oplossing ongelijk aan #\rv{0,0,0}# te vinden van het stelsel vergelijkingen \[\eqs{a\cdot p+b\cdot q+c&=&0\\ a\cdot r+b\cdot s+c&=&0\\ }\] in de onbekenden #a#, #b#, #c#.

Snijpunt

Snijpunten van lijnen zijn punten die op beide lijnen liggen. De snijpunten zijn dus oplossingen van elke vergelijking bij een van de twee lijnen. Andersom: elke oplossing van het stelsel van twee vergelijkingen, bestaande uit één vergelijking voor elke lijn, is een snijpunt.

Lijn door 2 punten

De lijn door twee verschillende punten #\rv{p,q}# en #\rv{r,s}# heeft een vergelijking van de vorm\[a\cdot x+b\cdot y+c=0\] voor zekere getallen #a#, #b#, #c# met ten minste één van #a#, #b# ongelijk aan #0#. De twee vergelijkingen in de stelling drukken het feit uit dat #\rv{p,q}# en #\rv{r,s}# oplossingen van de vergelijking moeten zijn.

Merk op dat #\rv{a,b,c}=\rv{0,0,0}# inderdaad tot gevolg heeft dat ten minste één van #a#, #b# ongelijk aan #0# is, want als #a=b=0#, dan forceren de gegeven vergelijkingen dat ook #c=0#.

De lijn door de twee punten #\rv{p,q}# en #\rv{r,s}# kan in één formule gegeven worden:

\[(q-s)\cdot x+(r-p)\cdot y+p\cdot s-q\cdot r= 0\]

Dit is eenvoudig na te gaan door invulling van de twee punten. Of door de vergelijkingen voor #a#, #b# en #c# op te lossen met #p#, #q#, #r# en #s# als parameters; dit levert #\rv{a,b,c}=\lambda\cdot \rv{q-s,r-p,p\cdot s-q\cdot r}# voor #\lambda\ne0#.

Hieronder staan voorbeelden van deze twee bewerkingen.

Bepaal de snijpunten van de twee lijnen gegeven door de vergelijkingen \(2x+3y-1=0\) en \(x+y-1=0 \).

Met andere woorden: wat is de oplossing van onderstaand stelsel vergelijkingen?
\[\eqs{2x+3y-1&=&0\\ x+y-1&=&0}\]

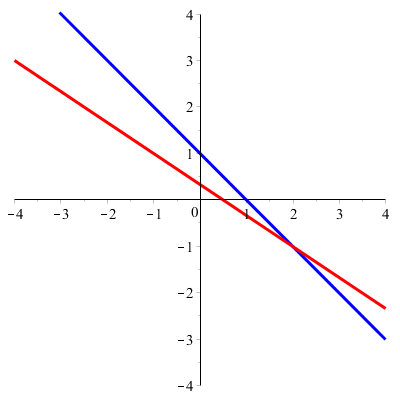
De lijnen snijden in het punt #\rv{2,-1}#

Door tweemaal de eerste vergelijking van de tweede af te trekken, ontstaat de vergelijking
\(y+1=0\), waaruit volgt #y=-1#. Invullen van deze waarde voor #y# in de eerste vergelijking geeft #2x-4=0#, waaruit volgt dat #x=2#. De oplossing van het stelsel is dus #x=2\land y= -1#. Dit betekent dat #\rv{x,y} = \rv{2,-1}# het snijpunt van de twee lijnen is.

In onderstaande figuur is de eerste lijn rood en de tweede blauw getekend.

Nieuw voorbeeld