Net zoals een lijn in het vlak beschreven wordt door een vergelijking in twee onbekende, wordt een vlak in de driedimensionale ruimte beschreven door een vergelijking in drie onbekenden:
Laat \(a\), \(b\), \(c\) en \(d\) reële getallen zijn. De oplossing van de vergelijking \[a\cdot x+b\cdot y+c\cdot z+d=0\] met onbekenden #x#, #y# en #z# kun je als verzameling punten in de driedimensionale ruimte beschouwen: ze bestaat uit alle punten \(\rv{x,y,z}\) die voldoen aan de genoemde vergelijking. Als tenminste één van #a#, #b#, #c# ongelijk aan #0# is, dan is de oplossing een vlak.
- Als \(c\ne0\), dan kunnen we de vergelijking schrijven als \(z=-\frac{a}{c}x-\frac{b}{c}y-\frac{d}{c}\). Immers, dit is de oplossing als we \(x\) en \(y\) als parameters beschouwen en \(z\) als onbekende. Het geeft aan dat er voor elke waarde van \(x\) en \(y\) een punt \(\rv{x,y,z}\) is met \(z\) gelijk aan \(-\frac{a}{c}x-\frac{b}{c}y-\frac{d}{c}\).
- Als \(a \ne 0\) of \(b \ne 0\) is sprake van een scheef vlak.
- Als \(a=0\) en \(b=0\), dan is de waarde van \(z\) overal gelijk aan \(-\frac{d}{c}\), en is sprake van een horizontaal vlak.
- In het uitzonderingsgeval \(c=0\) ziet de vergelijking er uit als \(a\cdot x+b\cdot y+d=0\).
- Als \(a \ne 0\) of \(b \ne 0\) is sprake van een verticaal vlak.
- Als \(a=0\) en \(b=0\) en
- \(d\ne 0\) dan zijn er geen oplossingen;
- \(d=0\) dan is elk drietal waarden voor \(x\), \(y\) en \(z\) een oplossing.
Een scheef vlak is de grafiek van de functie \(z(x,y)=-\frac{a}{c}x-\frac{b}{c}y-\frac{d}{c}\). Een verticaal vlak is de grafiek van de functie \(x(y,z) = -\frac{b}{a}y-\frac{c}{a}z-\frac{d}{a}\) als #a\ne0# en van de functie \(y(x,z) = -\frac{a}{b}x-\frac{c}{b}z-\frac{d}{b}\) als #b\ne0#.
We spreken van een vergelijking van een vlak omdat er meer vergelijkingen mogelijk zijn: voor elk getal \(k\ne 0\) beschrijven de vergelijkingen \(a\cdot x+b\cdot y+c\cdot z+d=0\) en \((k\cdot a)x+(k\cdot b)y+(k\cdot c)z+(k\cdot d)=0\) hetzelfde vlak.
Andersom is elk tweetal lineaire vergelijkingen in #x#, #y#, #z# dat hetzelfde vlak beschrijft, gelijk op een constant veelvoud na.
In termen van het inproduct #{\vec{u}}\boldsymbol{\cdot}{\vec{v}}=u_1\cdot v_1+u_2\cdot v_2+u_3\cdot v_3# kunnen we de vergelijking schrijven als
\[\rv{a,b,c}\boldsymbol{\cdot}\rv{x,y,z}=-d\]
Bijgevolg staat #\rv{a,b,c} # loodrecht op elke richtingsvector van het vlak. Daarom heet deze vector wel een normaalvector van het vlak. De normaalvector is uniek bepaald op scalaire veelvouden na.
Door vlakken door middel van lineaire vergelijkingen te beschrijven, kunnen we snijpunten van vlakken vinden als oplossingen van stelsels lineaire vergelijkingen.
De doorsnee (dat is de verzameling gemeenschappelijke snijpunten) van vlakken die beschreven worden door lineaire vergelijkingen in de coördinaten #x#, #y#, #z#, kunnen gevonden worden door het stelsel bestaande uit alle vergelijkingen bij deze vlakken op te lossen.
De doorsnee van twee verschillende vlakken die niet parallel zijn, is een lijn en kan beschreven worden met behulp van één enkele parameter.
Als meerdere verschillende vlakken een gemeenschappelijk snijpunt hebben, dan is hun doorsnee een punt of een lijn.
Een lijn kan beschreven worden door twee lineair vergelijkingen, die bij verschillende vlakken horen. Die vlakken zijn niet uniek bepaald: elk tweetal vlakken dat de lijn bevat, hoort bij een tweetal vergelijkingen dat de lijn beschrijft (dat wil zeggen: waarvan de oplossing de lijn is).
Vlakken zijn dan en slechts dan parallel als ze dezelfde normaalvectoren hebben. Twee vlakken hebben alleen in dat geval geen snijpunten.
Het is mogelijk dat drie niet-parallelle vlakken geen gemeenschappelijke snijpunten hebben. Een voorbeeld staat onderaan deze pagina.
Ook een vergelijking van het vlak door drie verschillende punten is te vinden door een stelsel lineaire vergelijkingen op te lossen:
Stel dat we drie verschillende punten in \(\mathbb{R}^3\) hebben die gerepresenteerd worden door de vectoren \(\vec{p}=\rv{p_1,p_2,p_3}\), \(\vec{q}=\rv{q_1,q_2,q_3}\) en \(\vec{r}=\rv{r_1,r_2,r_3}\). Dan heeft elk vlak door deze drie punten \(\vec{p}\), \(\vec{q}\) en \(\vec{r}\) een lineaire vergelijking van de vorm
\[a\cdot x+b\cdot y+c\cdot z+d=0\] waarbij #\rv{a, b, c,d}# een oplossing ongelijk aan #\rv{0,0,0,0}# is van het stelsel lineaire vergelijkingen
\[\eqs{ p_1\cdot a+ p_2\cdot b+ p_3\cdot c+d &=&0\\ q_1\cdot a+ q_2\cdot b+ q_3\cdot c+d &=&0\\ r_1\cdot a+ r_2\cdot b+ r_3\cdot c+d &=&0\\ }\]
Als de drie punten \(\vec{p}\), \(\vec{q}\) en \(\vec{r}\) op één lijn liggen, dan zijn er meer vlakken die aan de voorwaarden voldoen. Zoniet, dan is er precies één zo'n vlak en zijn de coëfficiënten #a#, #b#, #c#, #d# van de vergelijking van het vlak op een scalar na uniek bepaald.
Het vlak door drie punten #\vec{p}#, #\vec{q}# en #\vec{r}# heeft een vergelijking van de vorm\[a\cdot x+b\cdot y+c\cdot z + d=0\] voor zekere getallen #a#, #b#, #c#, #d# met ten minste één van #a#, #b#, #c# ongelijk aan #0#. De drie vergelijkingen in de stelling drukken het feit uit dat #\vec{p}#, #\vec{q}# en #\vec{r}# oplossingen van de vergelijking moeten zijn.
Merk op dat #\rv{a,b,c,d}=\rv{0,0,0,0}# inderdaad tot gevolg heeft dat ten minste één van #a#, #b#, #c# ongelijk aan #0# is, want als #a=b=c=0#, dan forceren de gegeven vergelijkingen dat ook #d=0#.
De constante term #d# kan weggewerkt worden door een van de vergelijkingen van een ander af te trekken. Met behulp van het inproduct kunnen we de resulterende vergelijkingen schrijven als \[\rv{a,b,c}\boldsymbol{\cdot}\left(\vec{p}-\vec{q}\right)=0\] voor de vergelijkingen waar #\vec{p}# en #\vec{q}# in voorkomen, en net zo voor de andere puntenparen. De normaalvector #\rv{a,b,c}# kan gevonden worden als oplossing van deze vergelijkingen.
De lineaire vergelijking kan expliciet beschreven worden:
\[ \begin{array}{rcl}\left( -{q_2}\,{r_3}+{p_2}\,{r_3}+{q_3}\,
{r_2}-{p_3}\,{r_2}-{p_2}\,{q_3}+{p_3}\,
{q_2} \right)\cdot x &&\\ + \left({q_1}\,{r_3}-\,{p_1}\,{r_3}-\,
{q_3}\,{r_1}+\,{p_3}\,{r_1}+\,{p_1}\,{q_3}
-\,{p_3}\,{q_1}\right) \cdot y&&\\ +\left(-{q_1}\,{r_2}+\,{p_1}\,
{r_2}+\,{q_2}\,{r_1}-\,{p_2}\,{r_1}-\,
{p_1}\,{q_2}+\,{p_2}\,{q_1}\right) \cdot z&& \\ + \left({p_1}\,
{q_2}\,{r_3}-\,{p_2}\,{q_1}\,{r_3}-\,{p_1}
\,{q_3}\,{r_2}+\,{p_3}\,{q_1}\,{r_2}+\,
{p_2}\,{q_3}\,{r_1}-\,{p_3}\,{q_2}\,{r_1}
\right) &=&0\end{array} \]
Maar het is handiger om het stelsel lineaire vergelijkingen met standaardtechnieken op te lossen dan om deze formule te onthouden.
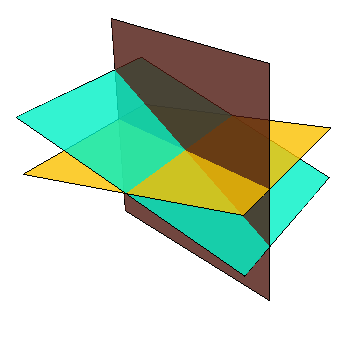
Gegeven zijn de drie vlakken:
\[\begin{array}{rcl} U &:\quad &x+2y=0\\ V &:\quad & x+2z=0\\ W&:\quad & z=0\end{array}\]
Bepaal waarin de drie vlakken #U#, #V#, #W# elkaar snijden.
De drie vlakken #U#, #V# en #W# snijden elkaar in het punt \(\rv{0,0,0}\).
Dit is in te zien door eerst #z=0# (de waarde vastgelegd door de derde vergelijking) in te vullen in de ander twee vergelijkingen, vervolgens #x=0# (de waarde vastgelegd door de nieuwe tweede vergelijking), en te constateren dat de eerste vergelijking nu forceert dat #y=0#.
De drie vlakken zijn in de figuur hieronder getekend.
 Vlakken in de ruimte
Vlakken in de ruimte





