Vector calculus in plane and space: The Cross Product
 Cross product in 3 dimensions
Cross product in 3 dimensions
As we know, the dot product of two vectors is a number, as is the cross product in two dimensions. In three dimensions, there is also a cross product. It gives a vector with special properties when there are two vectors in the space. This involves a vector perpendicular to both given vectors, but an orientation is also required: a rule that tells you where the cross product is pointing. We shall determine an orientation first.
Right-handed orientation
Three vectors #\vec{v}#, #\vec{w}#, #\vec{u}# (in this order), which are a basis of the space, are called right-handed oriented if #\vec{u}# is on the side of the plane through #\vec{0}#, #\vec{v}#, #\vec{w}# designated as follows by the middle finger: if #\vec{v}# can be found along the extended thumb, and #\vec{w}# lies along the extended index finger of the right hand, then the vector #\vec{u}# points toward the outstretched middle finger.
The figure below represents a right-handed oriented basis.
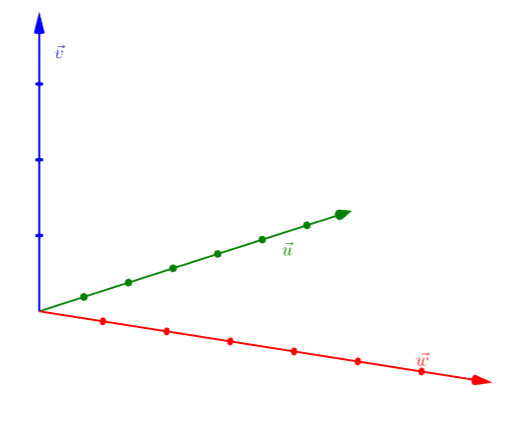
The way to see whether a basis is right-hand-oriented, is also known as the corkscrew rule.
If a basis is not right-hand-oriented, then there is only one other possibility: it is left-hand-oriented. If #\vec{v}#, #\vec{w}#, #\vec{u}# is right-hand-oriented, then #\vec{w}#, #\vec{v}#, #\vec{u}# is left-hand-oriented.
The cross product
The cross product #\vec{v} \times \vec{w}# of the vectors #\vec{v}# and #\vec{w}#, is the vector\[\vec{v}\times\vec{w}=\parallel\vec{v}\parallel\cdot\parallel\vec{w}\parallel\cdot \sin(\varphi)\cdot\vec{u}\] where
- #\varphi# is the short angle between #\vec{v}# and #\vec{w}# (so #0\leq \varphi \leq \pi#),
- #\vec{u}# is the vector of a length #1#, perpendicular to #\vec{v}# and #\vec{w}#, so #\vec{v}#, #\vec{w}#, #\vec{u}# is right-hand-oriented if #\varphi\ne0,\pi#.
The vectors #\vec{v}# and #\vec{w}# are then and only then on a single line through the origin if #\varphi=0# or #\pi# applies. In both cases, #\sin(\varphi) = 0#, so #\vec{v}\times\vec{w}=\vec{0}#. In this case, the orientation of the vectors #\vec{v}#, #\vec{w}#, and #\vec{u}# is not defined.
We choose #\vec{v}# and #\vec{w}# for the short angle. The oriented angle between #\vec{v}# and #\vec{w}# is actually undefined: the plane through the origin, #\vec{v}#, and #\vec{w}# does not, like any plane in space, necessarily have a top and bottom. In the two-dimensional theory, we see the plane from above, as it were. The oriented angle between the #x#-axis and #y#-axis, or rather between #\rv{1,0}# and #\rv{0,1}#, is measured by turning from one to the other counterclockwise. If we see these coordinates as the first two coordinates of the space, it corresponds to the right-handed basis #\rv{1,0,0}# (the #x#-axis), #\rv{0,1,0}# (the #y#-axis), and #\rv{0,0,1}# (the #z#-axis). Looking at the plane from above is described as looking from the position of third basis vector of a right-hand-oriented basis. In other words, only when we approach an orientation (such as 'counterclockwise' or '#\vec{v}# to #\vec{w}#') in the plane, can we speak of an oriented angle between two vectors. An oriented angle is not an obvious term, which explains why we avoid the oriented angle between #\vec{v}# and #\vec{w}# in the definition of the cross product in the space.
The scalar of the vector #\vec{u}# in the definition of the cross product will never be negative, for #\sin(\varphi)\ge0# because #\varphi# describes the short angle between #\vec{v}# and #\vec{w}#.
The length of #\vec{v}\times\vec{w}# is #\parallel\vec{v}\parallel\cdot\parallel\vec{w}\parallel\cdot\sin(\varphi)#. If the vectors #\vec{v}# and #\vec{w}#, for example, both have a length #4#, and the angle between the two vectors is equal to #60^{\circ}#, then
\[\vec{v}\times \vec{w} = 4\cdot 4\cdot \sin\left( 60^{\circ}\right) \cdot\vec{u}= 4\cdot 4\cdot \frac{1}{2}\sqrt{3}\cdot \vec{u}= 8\sqrt{3}\cdot\vec{u}
\] where #\vec{u}# is the unique vector of a length #1#, so #\vec{v}#, #\vec{w}#, #\vec{u}# is right-hand-oriented.
We come across other notations of the cross product in the literature, such as #\vec{v}\wedge\vec{w}#.
The cross product is also called the vector product.
The cross product in 2 dimensions of the vectors #\vec{v}# and #\vec{w}# satisfies #{\vec{v}\times\vec{w} } = {\parallel\vec{v}\parallel\cdot \parallel\vec{w}\parallel}\cdot \sin(\varphi) #. If we look at the plane as part of the space, then it is, except for a symbol, the scalar of the vector #\vec{u}# perpendicular to that plane which appears in the definition of the cross product in three dimensions above.
The cross product in terms of two lengths
Let #\vec{v}# and #\vec{w}# be two vectors that are not together on a line through the origin. Use #\vec{u}# to indicate the vector of a length #1# that is perpendicular to #\vec{v}# and #\vec{w}#, so #\vec{v}#, #\vec{w}#, and #\vec{u}# are right-hand-oriented. The cross product is then #\vec{v}\times\vec{w}# equal to #\lambda\cdot\vec{u}#, where #\lambda# is the product of the length #\parallel\vec{v}\parallel# of #\vec{v}# and the distance from the endpoint of #\vec{w}# to the line through #\vec{0}# with directional vector #\vec{v}#.
In particular, #\lambda# is either equal to double the area of the triangle with vertices #\vec{0}#, #\vec{v}#, and #\vec{w}#, or defined by the area of the parallelogram #\vec{v}# and #\vec{w}# (that is to say, with vertices #\vec{0}#, #\vec{v}#, #\vec{w}# and #\vec{v}+\vec{w}#).
This follows directly from the definition of #\sin(\varphi)# applied to the triangle #OAB# ,where #O# is the origin, #A# is the end point of the representative of #\vec{w}# with a starting point at the origin, and #B# is the perpendicular projection of #A# on the line through #O# and the end point of the representative of #\vec{v}# which is placed at the origin. See figure below.
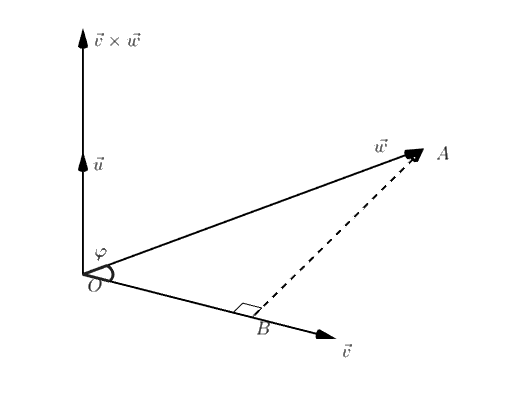
The last statement follows from the length-times-height law for the surface of a parallelogram, in which the length is equal to #\parallel\vec{v}\parallel# and the height is equal to #\parallel\vec{w}\parallel \cdot \sin( \varphi )#.
The formula for the cross product gives:
\[\vec{e}_{1}\times\vec{e}_{3}=\parallel\vec{e}_{1}\parallel\cdot\parallel\vec{e}_{3}\parallel\cdot \sin(\varphi)\cdot\vec{u}\] which
- #\varphi# the (shortest) angle between #\vec{e}_{1}# and #\vec{e}_{3}#,
- #\vec{u}# the vector of length #1# is perpendicular to #\vec{e}_{1}# and #\vec{e}_{3}#, such that #\vec{e}_{1}#, #\vec{e}_{3}#, #\vec{u}# is oriented right handed.
We can now determine the four factors of the right hand side of the formula as follows:
- The lengths #\parallel\vec{e}_{1}\parallel# and #\parallel\vec{e}_{3}\parallel# are both equal to #1# because the base is orthonormal.
- The sine of the angle #\varphi# is #1# because #\vec{e}_{1}# and #\vec{e}_{3}# are perpendicular.
- Vector #\vec{u}# is # - \vec{e}_{2}# because the three vectors #\vec{e}_1#, #\vec{e}_3#, #\vec{e}_2# are oriented left #{}#handed .

Or visit omptest.org if jou are taking an OMPT exam.



